浙江省金华市兰溪八中2023-2024学年七年级第一学期数学学习能力调查（一）试卷

试卷更新日期：2023-11-16 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 我国古代《九章算术》中注有“今两算得失相反，要令正负以名之”.是今有两数若其意义相反，则分别叫做正数与负数，如果向北走 $5$ 步记作 $+ 5$ 步，那么向南走 $10$ 步记作（　　）

A、 $+ 10$ 步 B、 $- 10$ 步 C、 $+ 12 步$ D、 $- 2$ 步

查看试题解析
2. 下列各选项中的两数互为相反数的是（）

A、-1和 $(- 1)^{3}$ B、-2和 $- \frac{1}{2}$ C、 $5$ 和 $| - 5 |$ D、-3和3

查看试题解析
3. 现在网购越来越多地成为人们的一种消费方式，在 $2022$ 年的“双 $11$ ”网上促销活动中天猫和淘宝的支付交易额突破 $57000000000$ 元，将数字 $57000000000$ 用科学记数法表示为（）

A、 $5.7 \times 1 0^{9}$ B、 $5.7 \times 1 0^{10}$ C、 $0.57 \times 1 0^{11}$ D、 $57 \times 1 0^{9}$

查看试题解析
4. 下列说法中正确的是（）

A、正分数和负分数统称为分数 B、正整数、负整数统称为整数 C、零既可以是正整数，也可以是负整数 D、一个有理数不是正数就是负数

查看试题解析
5. 下列说法不正确的是（）

A、近似数1.8与1.80表示的意义不同 B、0.0200精确到0.0001 C、5.0万精确到万位 D、1.0×10⁴精确到千位

查看试题解析
6. 在生产图纸上通常用 $\emptyset 30 0_{- 0.5}^{+ 0.2}$ 来表示轴的加工要求，这里 $\emptyset 300$ 表示直径是 $300 m m$ ， $+ 0.2$ 和 $- 0.5$ 是指直径在 $(300 - 0.5) m m$ 到 $(300 + 0.2) m m$ 之间的产品都属于合格产品.现加工一批轴，尺寸要求是 $\emptyset 4 5_{- 0.3}^{+ 0.2}$ ，则下面产品合格的是（）

A、 $44.6 m m$ B、 $44.8 m m$ C、 $45.3 m m$ D、 $45.5 m m$

查看试题解析
7. 在﹣ $\frac{7}{10}$ ， 0，﹣|﹣5|，﹣0.6，2，﹣（﹣ $\frac{1}{3}$ ），﹣10中负数的个数有（）

A、3 B、4 C、5 D、6

查看试题解析
8. 有理数a、b在数轴上的位置如图所示，则下列式子中成立的是（　　）

A、a+b＞0 B、a﹣b＞0 C、ab＞0 D、 $\frac{a}{b} < 0$

查看试题解析
9. 若 $a$ 与 $b$ 互为相反数， $c$ 与 $d$ 互为倒数，则 $- 2022 (a + b) - c d$ 的结果为（）

A、 $- 2022$ B、 $2022$ C、-1 D、1

查看试题解析
10. 数学上，为了简便把1到n的连续n个自然数的和记作 $\sum_{k = 1}^{n} k$ ，即 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + ⋯ + n$ ；把1到n的连续n个自然数的乘积记作n！，即n！＝1×2×3×…×（n﹣1）×n；则 $\sum_{i = 1}^{2020} i - \sum_{i = 1}^{2021} i + \frac{2021!}{2020!}$ 的值为（）

A、0 B、1 C、2020 D、2021

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）.

11. $\frac{2}{3}$ 的相反数是，倒数是，绝对值是.

查看试题解析
12. 比较大小： $- \frac{3}{4}$ $- \frac{2}{3}$ ； $3$ $- | 4 |$ .

查看试题解析
13. 已知（x-2）²+|y+1|＝0，则x+y＝．

查看试题解析
14. 若 $| m | = 7$ ，则 $m =$ ．

查看试题解析
15. 几个不是0的数相乘，负因数的个数是时，积是正数；负因数的个数是时，积是负数．

查看试题解析
16. 对于正整数a ，我们规定：若a为奇数，则f（a）＝5a﹣1；若a为偶数，则f（a）＝ $\frac{a}{2}$ ．例如f（3）＝5×3﹣1＝14，f（10）＝ $\frac{10}{2}$ ＝5．若 $a_{1}$ ＝8， $a_{2}$ ＝f（ $a_{1}$ ）， $a_{3}$ ＝f（ $a_{2}$ ）， $a_{4}$ ＝f（ $a_{3}$ ），…，依此规律进行下去，得到一列数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ …（n为正整数），则 $a_{3}$ ＝， $a_{1}$ + $a_{2}$ + $a_{3}$ +…+ $a_{2023}$ ＝．

查看试题解析

三、解答题（本大题共8小题，共66分）.

17. 计算：

(1)、 $（ - 7 ） - （ - 10 ）$ ；

(2)、 $3 \times （ - 1 ） - 4 \div （ - 2 ）$ ；

(3)、 $（ \frac{2}{3} + \frac{3}{4} - \frac{5}{6} ） \times （ - 12 ）$ ；

(4)、 $- 1^{4} - （ 1 - 0.5 ） \times \frac{1}{3} \times [2 - （ - 3 ）^{2}]$

查看试题解析
18. 把下列各数填入相应的横线上： $4$ ， $- 2 \frac{1}{2}$ ， $- 12$ ， $3.14159$ ， $0$ ， $\frac{2}{5}$
负数：｛｝；
非负数：｛｝；
整数：｛｝；
分数：｛｝。

查看试题解析
19. 观察数轴，回答下列问题：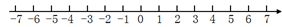

(1)、有没有最大或最小的整数？有没有最小的自然数？有没有最小的正整数和最大的负整数？如果有，请写出来.

(2)、不小于－3的负整数有哪些？

(3)、比－3小5的数是什么？比－3大5的数是什么？

(4)、－2和6的正中间的数是什么？

查看试题解析
20. 人的体重指数BMI可以用公式 $B M I = \frac{w}{h^{2}}$ 计算，其中w为人的体重（单位：kg），h为身高（单位：m）．由此可以用身高h的平方乘以体重指数BMI，得到体重w．中国成年人体重指数的标准如下：
当 $B M I < 18.5$ 时，为体重不足；
当 $18.5 \leq B M I < 24$ 时，为健康体重；
当 $24 \leq B M I < 28$ 时，为超重；
当 $B M I \geq 28$ 时，为肥胖．
小明爸爸的身高为1.73m，体重为75kg．通过计算解答下列问题（注：计算时取 $1.7 3^{2} \approx 3.0$ ）．

(1)、小明爸爸的体重指数BMI是多少？

(2)、当小明爸爸减掉3.5kg之后，他的体重是否成为了健康体重？说明理由．

查看试题解析
21. 红红有5张写着以下数字的卡片，请你按要求抽出卡片，完成下列各问题：

(1)、从中取出2张卡片，使这2张卡片上数字乘积最大，最大值是

(2)、从中取出2张卡片，使这2张卡片上数字相除的商最小，最小值是

(3)、从中取出除0以外的其他4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使运算结果为24（注：每个数字只能用一次，请写出两种符合要求的运算式子：
、

查看试题解析
22. 如图，一只甲虫在6×6的方格（每小格边长为1）上沿着网格线运动，它从A处出发去看望B、C、D处的其它甲虫，规定：向上和向右走为正，向下和向左走为负，例如：从A到B记为： $A \to B (+ 2 ， + 4)$ ，表示从A点先向右平移2个单位，再向上平移4个单位，反之从B到A记为： $B \to A (- 2 ， - 4)$ ，括号中第一个数表示左右方向，第二个数表示上下方向，那么图中：

(1)、 $C \to D$ （，）， $B \to C$ （，）， $D \to A$ （，）；

(2)、若这只甲虫的行走路线为 $A \to B \to C \to D$ ，则该甲虫走过的最少路程为；

(3)、若这只甲虫从A处去甲虫Р处的行走路线依次为 $(+ 1 ， + 2)$ ， $(+ 3 ， - 1)$ ， $(- 2 ， + 3)$ ， $(+ 4 ， 0)$ ，请在图中标出P的位置．

查看试题解析

23. 某路公交车从起点经过A、B、C、D站到达终点，一路上下乘客如下表所示．

（用正数表示上车的人数，负数表示下车的人数）

	起点	A	B	C	D	终点
上车的人数	18	15	12	7	5	0
下车的人数	0	-3	-4	-10	-11

(1)、到终点下车还有人；

(2)、车行驶在那两站之间车上的乘客最多？站和站；

(3)、若每人乘坐一站需买票1元，问该车出车一次能收入多少钱？请列出算式并写出计算过程．

查看试题解析

24. 综合与探究：
【概念学习】
现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如 $2 \div 2 \div 2$ ， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 等，类比有理数的乘方，我们把 $2 \div 2 \div 2$ 写作 $2^{③}$ ，读作“2的圈3次方”， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 写作 ${(- 3)}^{④}$ ，读作“ $(- 3)$ 的圈4次方”，一般地把 $\frac{a \div a \div a \div ⋯ \div a}{n 个 a} (a \neq 0)$ 写作 $a^{ⓝ}$ ，读作“a的圈n次方”．

(1)、【初步探究】
直接写出计算结果： $2^{③}$ =； ${(- \frac{1}{2})}^{③}$ = ．

(2)、【深入思考】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？
除方→ $2^{④}$ $= 2 \div 2 \div 2 \div 2 = 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}$ →乘方幂的形式
试一试：仿照上面的算式，把下列除方运算直接写成幂的形式： ${(- 3)}^{⑤}$ = ， ${(\frac{1}{5})}^{⑥}$ = ．

(3)、算一算： $1 2^{2} \div {(- \frac{1}{3})}^{④} \times (- 2)^{⑥} - {(- \frac{1}{3})}^{⑥} \div 3^{3}$ ．

查看试题解析