浙江省金华市义乌市五校2023-2024学年九年级第一学期第一次学情调查试卷

试卷更新日期：2023-11-16 类型：月考试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 若 $\frac{a}{b} = \frac{3}{4}$ ，则 $\frac{a + b}{b}$ =（）

A、2 B、 $\frac{7}{4}$ C、 $\frac{5}{4}$ D、 $\frac{3}{2}$

查看试题解析
2. 如果两个相似多边形面积的比为1：5，则它们的相似比为（）

A、1：25 B、1：5 C、1：2.5 D、1： $\sqrt{5}$

查看试题解析
3. 将抛物线 $y = - x^{2}$ 向左平移 $2$ 个单位后，得到的抛物线的表达式是（）

A、 $y = - (x + 2)^{2}$ B、 $y = - x^{2} + 2$ C、 $y = - (x - 2)^{2}$ D、 $y = - x^{2} - 2$

查看试题解析
4. 若 $△ A B C$ ∽ $△ A' B' C'$ ， $∠ A = 20 °$ ， $∠ B = 60 °$ ，则 $∠ C'$ 等于（）

A、 $20 °$ B、 $60 °$ C、 $100 °$ D、 $40 °$

查看试题解析
5. 对于二次函数 $y = - (x - 2)^{2} + 3$ 的图象与性质，下列说法正确的是（）

A、对称轴是直线 $x = 2$ ，最小值是 $3$ B、对称轴是直线 $x = 2$ ，最大值是 $3$ C、对称轴是直线 $x = - 2$ ，最小值是 $3$ D、对称轴是直线 $x = - 2$ ，最大值是 $3$

查看试题解析
6. 小颖用计算器探索方程 $a x^{2} + b x + c = 0$ 的根，作出如图所示的图象，并求得一个近似根 $x = - 3.4$ ，则方程的另一个近似根 $($ 精确到 $0.1)$ 为（）

A、 $4.4$ B、 $3.4$ C、 $2.4$ D、 $1.4$

查看试题解析
7. 如图，在平面直角坐标系中，已知点P（0，2），点A（4，2）．以点P为旋转中心，把点A按逆时针方向旋转60°，得点B ．在M₁（ $- \frac{\sqrt{3}}{3}$ ， 0），M₂（ $- \sqrt{3}$ ， ﹣1），M₃（1，4），M₄（2， $\frac{11}{2}$ ）四个点中，直线PB经过的点是（）

A、M₁ B、M₂ C、M₃ D、M₄

查看试题解析
8. 已知△ABC的三边长分别为6cm，7.5cm，9cm，△DEF的一边长为4cm，当△DEF的另两边长是下列哪一组时，这两个三角形相似（）

A、2cm，3cm B、4cm，5cm C、5cm，6cm D、6cm，7cm

查看试题解析
9. 如图，二次函数y=ax²+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0）．下列结论中，正确的一项是（）

A、 $a b c$ ＜0 B、 $2 a + b$ ＜0 C、 $a - b + c$ ＜0 D、4ac−b² $<$ 0

查看试题解析
10. 如图，将矩形 $A B C D$ 沿着 $G E$ 、 $E C$ 、 $G F$ 翻折，使得点 $A$ 、 $B$ 、 $D$ 恰好都落在点 $O$ 处，且点 $G$ 、 $O$ 、 $C$ 在同一条直线上，同时点 $E$ 、 $O$ 、 $F$ 在另一条直线上．小炜同学得出以下结论： $① G F / / E C$ ； $② A B = \frac{4 \sqrt{3}}{5} A D$ ； $③ G E = \sqrt{6} D F$ ； $④ O C = 2 \sqrt{2} O F$ ； $⑤ △ C O F$ ∽ $△ C E G$ ．其中正确的是（）

A、 $① ② ③$ B、 $① ③ ④$ C、 $① ④ ⑤$ D、 $② ③ ④$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 已知线段a=3，b=27，则a，b的比例中项线段长等于.

查看试题解析
12. 若抛物线 $y = x^{2} + b x + 3$ 经过点 $B (2 ， 3)$ ，则该抛物线的对称轴为．

查看试题解析
13. 已知 $P$ 是线段 $A B$ 的黄金分割点， $P A > P B$ ， $A B = 6 c m$ ，则 $P A =$ $c m$ ．

查看试题解析
14. 已知 $(- 3 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(1 ， y_{3})$ 是二次函数 $y = - 2 x^{2} - 8 x + m$ 图象上的点，比较 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小，用“＜”按从小到大顺序排列．

查看试题解析
15. 如果函数 $y = (k - 3) x^{k^{2} - 3 k + 2} + k x + 1$ 是二次函数，那么 $k$ 的值是．

查看试题解析
16. 对于二次函数 $y = a x^{2} + b x + c$ ，规定函数 $y = {\begin{array}{l} a x^{2} + b x + c (x \geq 0) \\ - a x^{2} - b x - c (x < 0) \end{array}$ 是它的相关函数.已知点 $M$ ， $N$ 的坐标分别为 $(- \frac{1}{2} ， 1)$ ， $(\frac{9}{2} ， 1)$ ，连接 $M N$ ，若线段 $M N$ 与二次函数 $y = - x^{2} + 4 x + n$ 的相关函数的图象有两个公共点，则 $n$ 的取值范围为．

查看试题解析

三、解答题（本题有8小题，共66分）

17. 计算：
|1- $\sqrt{2}$ |+ $\sqrt[3]{- 8}$ +（ $\frac{1}{3}$ ）^﹣2﹣（﹣4）+（-2）⁰；

查看试题解析
18. 如图，在方格纸中，每个小正方形的边长都是 $1$ ， $△ A B C$ 的三个顶点 $A$ ， $B$ ， $C$ 都在小方格的顶点上 $.$ 按照以下的要求画三角形．

(1)、在图 $①$ 中画一个格点三角形 $D E F$ ，使 $△ D E F$ ∽ $△ A B C$ ，且相似比为 $2 ∶ 1$ ；

(2)、在图 $②$ 中画一个格点三角形 $P Q R$ ，使 $△ P Q R$ ∽ $△ A B C$ ，且相似比为 $\sqrt{2} ∶ 1$ ．

查看试题解析
19. 某农场拟建三间矩形饲养室，饲养室一面靠现有墙 $($ 墙可用长 $\leq 20 m)$ ，中间用两道墙隔开，已知计划中的建筑材料可建围墙的总长为 $60 m$ ，设饲养室宽为 $x (m)$ ，总占地面积为 $y (m^{2}) ($ 如图所示 $)$ ．

(1)、求 $y$ 关于 $x$ 的函数表达式，并直接字写出自变量 $x$ 的取值范围；

(2)、三间饲养室占地总面积有可能达到 $210 | m^{2}$ 吗？请说明理由．

查看试题解析
20. 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C.

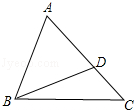(1)、求证：△ABD∽△ACB

(2)、若AB=6，AD=4，求线段CD的长

查看试题解析
21. 如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm．动点M从点B出发，在BA边上以每秒3cm的速度向定点A运动，同时动点N从点C出发，在CB边上以每秒2cm的速度向点B运动，且MG⊥BC，运动时间为t秒（0＜t＜ $\frac{10}{3}$ ），连接MN．

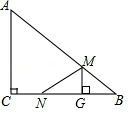(1)、用含t的式子表示MG；

(2)、当t为何值时，四边形ACNM的面积最小？并求出最小面积；

(3)、若△BMN与△ABC相似，求t的值．

查看试题解析
22. 已知关于 $x$ 的一元二次方程 $x^{2} + (k - 5) x + 1 - k = 0$ ，其中 $k$ 为常数．

(1)、求证：无论 $k$ 为何值，方程总有两个不相等实数根；

(2)、已知函数 $y = x^{2} + (k - 5) x + 1 - k$ 的图象不经过第三象限，求 $k$ 的取值范围；

(3)、若原方程的一个根大于 $3$ ，另一个根小于 $3$ ，求 $k$ 的最大整数值．

查看试题解析
23. 如图：

(1)、【问题初探】
如图1， $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D是 $B C$ 上一点，连接 $A D$ ，以 $A D$ 为一边作 $Δ A D E$ ，使 $∠ D A E = 90 °$ ， $A D = A E$ ，连接 $B E$ ， $B E$ 与 $C D$ 的数量关系，位置关系．

(2)、【类比再探】
如图2， $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点M是 $A B$ 上一点，点D是 $B C$ 上一点，连接 $M D$ ，以 $M D$ 为一边作 $Δ M D E$ ，使 $∠ D M E = 90 °$ ， $M D = M E$ ，连接 $B E$ ，求 $∠ E B D$ 的度数．

(3)、【方法迁移】
如图3， $R t Δ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 30 °$ ， $B C = 6$ ，点M是 $A B$ 中点，点D是 $B C$ 上一点且 $B D = 1$ ，连接 $M D$ ，以 $M D$ 为一边作 $Δ M D E$ ，使 $∠ D M E = 90 °$ ， $M D = \sqrt{3} M E$ ，连接 $B E$ ，求 $B E$ 的长．

查看试题解析
24. 如图，已知抛物线y＝ax²+bx+6经过两点A（﹣1，0），B（3，0），C是抛物线与y轴的交点.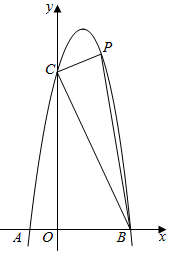

(1)、求抛物线的解析式；

(2)、点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，设△PBC的面积为S，求S关于m的函数表达式（指出自变量m的取值范围）和S的最大值；

(3)、点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N使得∠CMN＝90°，且△CMN与△OBC相似，如果存在，请求出点M和点N的坐标.

查看试题解析