浙江省宁波市海曙区2023-2024学年九年级上学期数学10月月考试卷

试卷更新日期：2023-11-16 类型：月考试卷

进入出卷网下载

一、选择题（每小题4分，共40分）

1. 下列函数是二次函数的是（）

A、y＝2x B、y＝x+1 C、y＝ $\frac{1}{x}$ D、y＝x²

查看试题解析
2. 二次函数 $y = (x - 1)^{2} - 2$ 的顶点坐标是（）

A、 $(- 1 ， 2)$ B、 $(1 ， - 2)$ C、 $(- 1 ， - 2)$ D、 $(1 ， 2)$

查看试题解析
3. 已知 $⊙ O$ 的半径为4，点A到圆心O的距离为6，则点A与 $⊙ O$ 的位置关系是（）

A、点A在圆内 B、点A在圆上 C、点A在圆外 D、无法确定

查看试题解析
4. 将二次函数 $y = x^{2} - 2 x - 3$ 的图象，先向右平移2个单位，再向上平移2个单位后的函数
表达式为（）

A、 $y = {(x - 3)}^{2} - 6$ B、 $y = {(x + 1)}^{2} - 6$ C、 $y = {(x + 1)}^{2} - 2$ D、 $y = {(x - 3)}^{2} - 2$

查看试题解析
5. 如图，在4×4正方形网格中，任意选取一个白色的小正方形并涂上阴影，使图中阴影部分的图形构成一个轴对称图形的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{12}$

查看试题解析
6. 已知二次函数y＝（x﹣2）²+2，当点（3，y₁）、（2.5，y₂）、（4，y₃）在函数图象上时，则y₁、y₂、y₃的大小关系正确的是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₂＜y₁＜y₃

查看试题解析
7. 如图，⊙O的直径CD垂直弦 $A B$ 于点E ，且 $C E = 3 ， D E = 7$ ，则 $A E =$ （）

A、 $\sqrt{21}$ B、2 C、4 D、 $\sqrt{29}$

查看试题解析
8. 如图，⊙O的直径AB与弦CD的延长线交于点E ，若DE＝OB ， ∠AOC＝84°，则∠E等于（）

A、28° B、42° C、21° D、20°

查看试题解析
9. 抛物线y＝ax²﹣a（a≠0）与直线y＝kx交于A（x₁ ， y₁），B（x₂ ， y₂）两点，若x₁+x₂＜0，则直线y＝ax+k一定经过（）

A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限

查看试题解析
10. 二次函数y＝ax²+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：（1）abc＜0；（2）4a+c＞2b；（3）3b﹣2c＞0；（4）若点A（﹣2，y₁）、点B（﹣ $\frac{1}{2}$ ， y₂）、点C（ $\frac{7}{2}$ ， y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）4a+2b≥m（am+b）（m为常数）.其中正确的结论有（）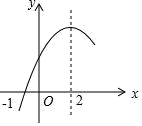

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题（每小题5分，共30分）

11. 一个仅装有球的不透明布袋里只有6个红球和 $n$ 个白球（仅有颜色不同）．若从中任意摸出一个球是红球的概率为 $\frac{2}{5}$ ，则 $n =$ ．

查看试题解析
12. ⊙O外一点P到⊙O上的点的最大距离是12，最小距离是2，求此圆的半径是

查看试题解析
13. 如图，在△ABC中，AB＝AC＝12cm，∠BAC＝50°，以AB为直径作半圆，交BC于点D，交AC于点E，则弧DE的长为cm．

查看试题解析
14. 抛物线y＝﹣ $\frac{1}{2}$ （x+5）²+2关于原点对称的抛物线的解析式为．

查看试题解析
15. 已知抛物线y＝﹣4x²+4mx﹣4m﹣m²（m是常数），若0≤x≤1时，函数y有最大值﹣5，则m的值为

查看试题解析
16. 如图，AB是半圆O的直径，点C在半圆上，AB＝13，AC＝12，D是 $\overset{⌢}{B C}$ 上的一个动点，连接AD．过点C作CE⊥AD于E，连接BE，则BE的最小值是．

查看试题解析

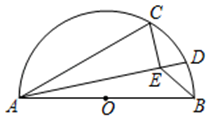
三、解答题

17. 若函数 $y = (m - 3) x^{m^{2} - 7} - x + 3$ 是关于 $x$ 的二次函数，求m的值？

查看试题解析
18. 某校对A ．《三国演义》、B ．《红楼梦》、C ．《西游记》、D ．《水浒传》四大名著开展“传统文化经典著作”推荐阅读活动．

(1)、小云从这4部名著中，随机选择1部阅读，他选中《红楼梦》的概率为．

(2)、该校拟从这4部名著中，选择2部作为课外阅读书籍．请用画树状图的方法求《红楼梦》被选中的概率．

查看试题解析
19. 如图，已知AB是⊙O的弦，C是 $\hat{A B}$ 的中点，AB=8，AC=2 $\sqrt{5}$ ，求⊙O半径的长.

查看试题解析
20. 如图，二次函数 $y_{1} = a x^{2} + b x + 3$ 的图象与x轴相交于点A（﹣3，0），B（﹣1，0），与y轴相交于点C．

(1)、求二次函数的表达式和其图象的顶点坐标．

(2)、若一次函数y₂＝kx+3的图象经过二次函数图象的顶点，请根据图象直接写出当y₁＞y₂时x的取值范围．

查看试题解析
21. 如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D， $\overset{⌢}{A B} = \overset{⌢}{A E}$ ， BE分别交AD，AC于点F，G.

(1)、求证：FA＝FG；

(2)、若BD＝DO＝3，求弧EC的长度．

查看试题解析
22. 某商场销售一种小商品，进货价为40元/件．当售价为60元/件时，每天的销售量为300件．在销售过程中发现：销售单价每上涨4元，每天的销售量就减少40件．设销售价格上涨x元/件（x为偶数），每天的销售量为y件．

(1)、当销售价格上涨10元时，每天对应的销售量为件．

(2)、请写出y与x的函数关系式．

(3)、设每天的销售利润为w元，为了让利于顾客，则每件商品的销售单价定为多少元时，每天获得的利润最大，最大利润是多少？

查看试题解析
23. 定义：若圆内接三角形是等腰三角形，我们就称这样的三角形为“圆等三角形”．

(1)、如图1，AB是⊙O的一条弦（非直径），若⊙O在上找一点C，使得△ABC是“圆等三角形”，则这样的点C能找到个．

(2)、如图2，四边形ABCD是⊙O的内接四边形，连结对角线BD，△ABD和△BCD均为“圆等三角形”，且AB=AD．
①当∠A=140°时，求∠ADC的度数；
②如图3，当∠A=120°，AB=6时，求阴影部分的面积．

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + c$ （a≠0）的对称轴为直线x＝﹣1，且抛物线经过A（2，0），C（0，4）两点，与x轴交于点B．

(1)、若直线y＝mx+n经过B ， C两点，求直线BC和抛物线的解析式；

(2)、在抛物线的对称轴x＝﹣1上找一点M ，使MA+MC的值最小，求点M的坐标；

(3)、设P为抛物线的对称轴x＝﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标，直接写出点P的坐标。

查看试题解析