安徽省淮南市凤台县2023-2024学年九年级上学期月考数学试卷(10月份)
试卷更新日期:2023-11-15 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列关于的函数中,是二次函数的是( )A、 B、 C、 D、2. 若是一元二次方程的一个根,则的值为( )A、 B、 C、 D、3. 下列函数中,当时,随的增大而增大的是( )A、 B、 C、 D、4. 一元二次方程的根的情况是( )A、无实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 抛物线与抛物线的相同点是( )A、顶点相同 B、对称轴相同 C、抛物线形状相同 D、顶点都在轴上6. 利用“配方法”解一元二次方程 , 配方后,得( )A、 B、 C、 D、7. 在同一平面直角坐标系中,直线是常数且与抛物线的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 8. 若等腰三角形不等边的一边长为 , 另两边长是关于的方程的两个根,则的值为( )A、 B、或 C、或 D、9. 抛物线是常数且的图象如图所示,下列结论正确的是( )
8. 若等腰三角形不等边的一边长为 , 另两边长是关于的方程的两个根,则的值为( )A、 B、或 C、或 D、9. 抛物线是常数且的图象如图所示,下列结论正确的是( )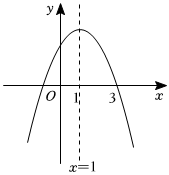 A、 B、 C、 D、10. 如图,点和点同时从正方形的顶点出发,点沿着运动,点沿着运动,速度都为 , 终点都是点若 , 则的面积与运动时间之间的函数关系的图象大致是( )
A、 B、 C、 D、10. 如图,点和点同时从正方形的顶点出发,点沿着运动,点沿着运动,速度都为 , 终点都是点若 , 则的面积与运动时间之间的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共4小题,共20.0分)
-
11. 关于的一元二次方程化为一般形式是 .12. 若抛物线的顶点在轴上,则的值是 .13. 如图,下列图形是由相同的小圆组成的,观察图形的变化:
第个图形:
 ;
;第个图形:
 ;
;第个图形:
 ;
;第个图形:
 ;
;若第个图形有个小圆,则的值为 .
14. 已知抛物线是常数且 .(1)、该抛物线的对称轴为直线 ;(2)、当时,将抛物线向左平移个单位长度,使抛物线经过原点,则的值为 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 用合适的方法解方程: .16. 已知二次函数 .(1)、填写下列表格:(2)、在下列平面直角坐标系中画出该二次函数的图象.
 17. 已知抛物线 .(1)、求该抛物线的开口方向、对称轴及顶点坐标;(2)、当为何值时,随的增大而减小,当为何值时,随的增大而增大?18. 某西瓜地种植一种优质无籽西瓜,随着种植技术的改进,产量从的增加到年的 .(1)、求这种无籽西瓜平均每年增产的百分率;(2)、若平均每年增产率不变,年该西瓜地的无籽西瓜产量能突破吗?19. 如图,在正方形中,轴,点 , 点已知抛物线是常数且经过点与点 , 且顶点位于上若抛物线与轴交于点 , 求的长.
17. 已知抛物线 .(1)、求该抛物线的开口方向、对称轴及顶点坐标;(2)、当为何值时,随的增大而减小,当为何值时,随的增大而增大?18. 某西瓜地种植一种优质无籽西瓜,随着种植技术的改进,产量从的增加到年的 .(1)、求这种无籽西瓜平均每年增产的百分率;(2)、若平均每年增产率不变,年该西瓜地的无籽西瓜产量能突破吗?19. 如图,在正方形中,轴,点 , 点已知抛物线是常数且经过点与点 , 且顶点位于上若抛物线与轴交于点 , 求的长. 20. 解高次方程的思想就是“降次”,将含未知数的某部分用低次项替换,称为换元法,例如解四次方程时,可设 , 则原方程可化为 , 解得 , , 当时,则 , 无实数根;当时,即 , 则 , 根据上述方法,完成下列问题:(1)、设 , 将方程转化为一元二次方程,得 ;(2)、解方程: .21. 如图,已知抛物线是常数且 , 对称轴为直线
20. 解高次方程的思想就是“降次”,将含未知数的某部分用低次项替换,称为换元法,例如解四次方程时,可设 , 则原方程可化为 , 解得 , , 当时,则 , 无实数根;当时,即 , 则 , 根据上述方法,完成下列问题:(1)、设 , 将方程转化为一元二次方程,得 ;(2)、解方程: .21. 如图,已知抛物线是常数且 , 对称轴为直线 (1)、求抛物线与轴交点的另一坐标;(2)、若关于的一元二次方程有两个不相等的实数根,根据图象直接写出的取值范围为 ;(3)、当时,的取值范围为 ,若点 , , 都在该抛物线上,用“”连接 , 和得 .22. 如图 , 张爷爷用长的隔离网在一段长的院墙边围成矩形养殖园,已知矩形的边靠院墙,和与院墙垂直,设的长为xm.
(1)、求抛物线与轴交点的另一坐标;(2)、若关于的一元二次方程有两个不相等的实数根,根据图象直接写出的取值范围为 ;(3)、当时,的取值范围为 ,若点 , , 都在该抛物线上,用“”连接 , 和得 .22. 如图 , 张爷爷用长的隔离网在一段长的院墙边围成矩形养殖园,已知矩形的边靠院墙,和与院墙垂直,设的长为xm. (1)、当围成的矩形养殖园面积为时,求的长;(2)、如图 , 张爷爷打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道隔离网已知两道隔离网与院墙垂直,请问此时养殖园的面积能否达到?若能,求出的长;若不能,请说明理由.23. 如图,抛物线是常数且经过点 , 该抛物线的对称轴为直线 .
(1)、当围成的矩形养殖园面积为时,求的长;(2)、如图 , 张爷爷打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道隔离网已知两道隔离网与院墙垂直,请问此时养殖园的面积能否达到?若能,求出的长;若不能,请说明理由.23. 如图,抛物线是常数且经过点 , 该抛物线的对称轴为直线 . (1)、求该抛物线的解析式;(2)、点是抛物线的顶点坐标,与轴交于点 , 抛物线与轴交于点 .
(1)、求该抛物线的解析式;(2)、点是抛物线的顶点坐标,与轴交于点 , 抛物线与轴交于点 .(ⅰ)若点是抛物线对称轴上一点,求的最小值;
(ⅱ)y轴上是否存在点 , 使得的面积为?若存在,请求点的坐标;若不存在,请说明理由.