安徽省六安市金安区重点中学2023-2024学年九年级上学期月考数学试卷(10月份)
试卷更新日期:2023-11-15 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 下列度数可能是n边形内角和的是( )A、300° B、550° C、900° D、960°3. 将方程配方后,原方程变形为( )A、 B、 C、 D、4. 若反比例函数的图象经过点 , 则的值是( )A、 B、 C、 D、5. 下列函数中,随增大而增大的是( )A、 B、 C、 D、6. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
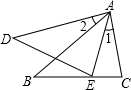 A、∠C=∠AED B、∠B=∠D C、 D、7. 如图,在中,为上一点,若 , , 则的值为( )
A、∠C=∠AED B、∠B=∠D C、 D、7. 如图,在中,为上一点,若 , , 则的值为( ) A、 B、 C、 D、8. 义务教育课程标准年版首次把学生学会炒菜纳入劳动教育课程,并作出明确规定某班有名学生已经学会炒的菜品的种数依次为: , , , , , , 则这组数据的众数和中位数分别是( )A、 , B、 , C、 , D、 ,9. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )
A、 B、 C、 D、8. 义务教育课程标准年版首次把学生学会炒菜纳入劳动教育课程,并作出明确规定某班有名学生已经学会炒的菜品的种数依次为: , , , , , , 则这组数据的众数和中位数分别是( )A、 , B、 , C、 , D、 ,9. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )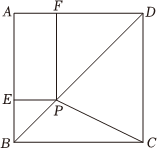 A、 B、 C、 D、10. 如图,已知抛物线的对称轴为 , 过其顶点的一条直线与该抛物线的另一个交点为要在坐标轴上找一点 , 使得的周长最小,则点的坐标为( )
A、 B、 C、 D、10. 如图,已知抛物线的对称轴为 , 过其顶点的一条直线与该抛物线的另一个交点为要在坐标轴上找一点 , 使得的周长最小,则点的坐标为( ) A、 B、 C、或 D、以上都不正确
A、 B、 C、或 D、以上都不正确二、填空题(本大题共4小题,共20.0分)
-
11. 已知 , , , 是成比例线段,期中 , , , 则 .12. 如图,抛物线的对称轴是直线 , 与轴的一个交点为 , 抛物线和与轴的另一个交点为 .
 13. 如图,、是函数上两点,为一动点,作轴,轴,若 , 则 .
13. 如图,、是函数上两点,为一动点,作轴,轴,若 , 则 . 14. 如图,点是菱形的边的中点,点是上的一点,点是上的一点,先以为对称轴将折叠,使点落在上的点处,再以为对称轴折叠 , 使得点的对应点与点重合,以为对称轴折叠 , 使得点的对应点落在上,则:
14. 如图,点是菱形的边的中点,点是上的一点,点是上的一点,先以为对称轴将折叠,使点落在上的点处,再以为对称轴折叠 , 使得点的对应点与点重合,以为对称轴折叠 , 使得点的对应点落在上,则: (1)、 ;(2)、若 , 则的值为 .
(1)、 ;(2)、若 , 则的值为 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算: .16. 已知线段a、b、c,且 .(1)、求 的值;(2)、若线段a、b、c满足 ,求a、b、c的值.17. 如图, , 与交于点 , 且. , , .
 (1)、求的长.(2)、求证:∽ .18. 已知抛物线 .(1)、求证:此抛物线与轴必有两个不同的交点;(2)、若此抛物线与直线的一个交点在轴上,求的值.19. 如图,在平面直角坐标系中,直线:与反比例函数的图象交于、两点,与轴相交于点 , 已知点 , 的坐标分别为和 .
(1)、求的长.(2)、求证:∽ .18. 已知抛物线 .(1)、求证:此抛物线与轴必有两个不同的交点;(2)、若此抛物线与直线的一个交点在轴上,求的值.19. 如图,在平面直角坐标系中,直线:与反比例函数的图象交于、两点,与轴相交于点 , 已知点 , 的坐标分别为和 . (1)、求反比例函数的解析式;(2)、直接写出不等式的解集;(3)、点为反比例函数图象上任意一点,若 , 求点的坐标.20. 如图,四边形是平行四边形,对角线、相交于点 , 点、分别在、上, , 连接 , 且 .
(1)、求反比例函数的解析式;(2)、直接写出不等式的解集;(3)、点为反比例函数图象上任意一点,若 , 求点的坐标.20. 如图,四边形是平行四边形,对角线、相交于点 , 点、分别在、上, , 连接 , 且 .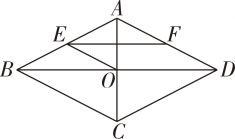 (1)、求证:四边形是菱形;
(1)、求证:四边形是菱形;
(2)、连接 , 若点是的中点, , , 求四边形的面积.21. 某校开展数学竞赛竞赛成绩为百分制 , 并随机抽取了名学生的竞赛成绩本次竞赛没有满分 , 经过整理数据得到以下信息:信息一:名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组每组数据含前端点值,不含后端点值 .
信息二:第三组的成绩单位:分为: , , , , , , , , , , , .

根据信息解答下列问题:
(1)、补全第二组频数分布直方图直接在图中补全;(2)、第三组竞赛成绩的众数是 分,抽取的名学生竞赛成绩的中位数是 分;(3)、若该校共有名学生参赛,请估计该校参赛学生成绩不低于分的人数.22. 如图,在中,、为边上的两个动点, .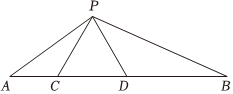 (1)、若即、重合 , 则 时,∽;(2)、若 , , 则与相似吗?为什么?(3)、当和满足怎样的数量关系时,∽?请说明理由.23. 某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元件设第个生产周期设备的售价为万元件,售价与之间的函数解析式是 , 其中是正整数当时,;当时, .(1)、求 , 的值;(2)、设第个生产周期生产并销售完设备的数量为件,且与满足关系式 .
(1)、若即、重合 , 则 时,∽;(2)、若 , , 则与相似吗?为什么?(3)、当和满足怎样的数量关系时,∽?请说明理由.23. 某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元件设第个生产周期设备的售价为万元件,售价与之间的函数解析式是 , 其中是正整数当时,;当时, .(1)、求 , 的值;(2)、设第个生产周期生产并销售完设备的数量为件,且与满足关系式 .当时,工厂第几个生产周期获得的利润最大?最大的利润是多少万元?
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.