江西省上饶市弋阳县2023-2024学年七年级上学期第一次月考数学试卷
试卷更新日期:2023-11-15 类型:月考试卷
一、选择题(本大题共6小题,共18.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的倒数是( )A、 B、 C、 D、2. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )A、0.28×1013 B、2.8×1011 C、2.8×1012 D、28×10113. 下列说法正确的是( )A、任何有理数的绝对值一定是正数 B、正数和负数统称为有理数 C、乘积为的两个数互为倒数 D、最大的负整数是4. 如图,数轴上被墨水遮盖的数的绝对值可能是( )
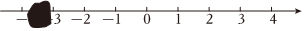 A、 B、 C、 D、5. 数轴上某一个点表示的数为 , 比小的数用表示,那么的最小值为( )A、 B、 C、 D、6. 如 , 我们叫集合 , 其中 , , 叫做集合的元素.集合中的元素具有确定性如必然存在 , 互异性如 , , 无序性即改变元素的顺序,集合不变若集合 , 我们说已知集合 , 集合 , 若 , 则的值是( )A、 B、 C、 D、
A、 B、 C、 D、5. 数轴上某一个点表示的数为 , 比小的数用表示,那么的最小值为( )A、 B、 C、 D、6. 如 , 我们叫集合 , 其中 , , 叫做集合的元素.集合中的元素具有确定性如必然存在 , 互异性如 , , 无序性即改变元素的顺序,集合不变若集合 , 我们说已知集合 , 集合 , 若 , 则的值是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
7. 升降机在陨星过程中,如果上升米记作“米”,那么下降米记作 米8. 计算: .9. 用“”、“=”、“”符号填空: .10. 已知 ,则 =.11. 若a与b互为相反数,c和d互为倒数,m的绝对值是2,则的值为 .12. 点在数轴上,点所对应的数用表示,且点到原点的距离等于 , 则的值为 .
三、解答题(本大题共11小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
13. 计算:(1)、;(2)、 .14. 在数轴上表示下列各数: , , , , 并将它们按从小到大的顺序用“”排列起来.
 15. 计算 , 嘉琪同学的计算过程如下,原式请你判断嘉琪的计算过程是否正确,若不正确,请你写出正确的计算过程.16. 如图,数轴上点 , , , 表示的数分别为 , , , , 相邻两点间的距离均为个单位长度.
15. 计算 , 嘉琪同学的计算过程如下,原式请你判断嘉琪的计算过程是否正确,若不正确,请你写出正确的计算过程.16. 如图,数轴上点 , , , 表示的数分别为 , , , , 相邻两点间的距离均为个单位长度. (1)、若与互为相反数,则 ;(2)、若这四个数中最小数与最大数的和等于 , 求的值.17. 已知有理数 , , 的位置如图所示.
(1)、若与互为相反数,则 ;(2)、若这四个数中最小数与最大数的和等于 , 求的值.17. 已知有理数 , , 的位置如图所示. (1)、用“”或“”填空: ,(2)、化简式子: .18. 为了增强体质,小明给自己设定:以每天跑步千米为基准,超过的部分记为正,不足的部分记为负,手机应用程序统计小明一周跑步情况,记录如下:
(1)、用“”或“”填空: ,(2)、化简式子: .18. 为了增强体质,小明给自己设定:以每天跑步千米为基准,超过的部分记为正,不足的部分记为负,手机应用程序统计小明一周跑步情况,记录如下:星期
一
二
三
四
五
六
日
与基准的差千米
小明周六和周日共跑了千米.
(1)、求的值.(2)、小明本周共跑了多少千米?19. 一架飞机进行特技表演,起飞后的高度变化如下表:高度变化
上升
下降
上升
下降
上升
记作
(1)、求此时飞机比起飞点高了多少千米?(2)、若飞机平均上升千米需消耗升燃油,平均下降千米需消耗升燃油,那么这架飞机在这个特技动作表演过程中,一共消耗多少升燃油?20. 用直尺画数轴时,数轴上的点 , , 分别代表数字 , , , 已知 , , 如图所示,设点 , 该轴的原点为 . (1)、若点所表示的数是 , 则点所表示的数是 ;(2)、若点 , 所表示的数互为相反数,则点所表示的数是 ,此时的值为 ;(3)、若数轴上点到原点的距离为 , 求的值.21. 如图 , 边长为的大正方形有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示
(1)、若点所表示的数是 , 则点所表示的数是 ;(2)、若点 , 所表示的数互为相反数,则点所表示的数是 ,此时的值为 ;(3)、若数轴上点到原点的距离为 , 求的值.21. 如图 , 边长为的大正方形有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示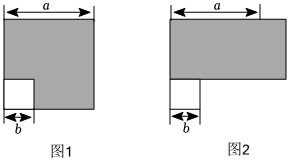 (1)、观察左、右两图的阴影部分面积,可以得到公式 ;(2)、已知 , , 则 ;(3)、请应用这个公式完成下列计算: .22. 先阅读下面材料,再完成任务:
(1)、观察左、右两图的阴影部分面积,可以得到公式 ;(2)、已知 , , 则 ;(3)、请应用这个公式完成下列计算: .22. 先阅读下面材料,再完成任务:【材料】
下列等式: , , …,具有的结构特征,我们把满足这一特征的一对有理数称为“共生有理数对”,记作 . 例如:、都是“共生有理数对”.
【任务】
(1)、在两个数对、中,“共生有理数对”是 .(2)、请再写出一对“共生有理数对”;(要求:不与题目中已有的“共生有理数对”重复)(3)、若是“共生有理数对”,求x的值;(4)、若是“共生有理数对”,判断是不是“共生有理数对”,并说明理由.23. 如图,已知数轴上点表示的数为 , 是数轴上在左侧的一点,且 , 两点间的距离为动点从点出发,以每秒个单位长度的速度沿数轴向左匀速运动,设运动时间为秒. (1)、数轴上点表示的数是 , 点表示的数是用含的代数式表示;(2)、动点从点出发,以每秒个单位长度的速度沿数轴向左匀速运动,若点、同时出发.求:
(1)、数轴上点表示的数是 , 点表示的数是用含的代数式表示;(2)、动点从点出发,以每秒个单位长度的速度沿数轴向左匀速运动,若点、同时出发.求:①当点运动多少秒时,点与点相遇?
②当点运动多少秒时,点与点间的距离为个单位长度?