北京市重点大学附中2023-2024学年九年级上学期月考数学试卷（10月份）

试卷更新日期：2023-11-15 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1. 抛物线 $y = (x - 3)^{2} + 1$ 的顶点坐标是（）

A、 $(- 3 ， 1)$ B、 $(3 ， 1)$ C、 $(- 3 ， - 1)$ D、 $(3 ， - 1)$

查看试题解析
2. 用配方法解一元二次方程 $x^{2} - 6 x + 4 = 0$ ，配方正确的是（）

A、 $(x + 3)^{2} = 13$ B、 $(x + 3)^{2} = 5$ C、 $(x - 3)^{2} = 13$ D、 $(x - 3)^{2} = 5$

查看试题解析
3. 将抛物线 $y = 3 x^{2}$ 先向左平移1个单位，再向下平移2个单位，所得抛物线的表达式为（）

A、 $y = 3 (x - 1)^{2} + 2$ B、 $y = 3 (x + 1)^{2} - 2$ C、 $y = 3 (x + 1)^{2} + 2$ D、 $y = 3 (x - 1)^{2} - 2$

查看试题解析
4. 如图，平面直角坐标系 $x O y$ 中， $A (- 4 ， 0)$ ， $B (0 ， 3)$ ，点 $P$ 为线段 $A B$ 的中点，则线段 $O P$ 的长为（）

A、 $\frac{3}{2}$ B、 $2$ C、 $\frac{5}{2}$ D、 $5$

查看试题解析
5. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $x_{1} + x_{2} - x_{1} \cdot x_{2}$ 的值是（）

A、 $1$ B、 $3$ C、 $- 1$ D、 $- 3$

查看试题解析
6. 关于 $x$ 的一元二次方程 $(a - 5) x^{2} - 4 x - 1 = 0$ 有实数根，则 $a$ 满足（）

A、 $a \geq 1$ B、 $a > 1$ 且 $a \neq 5$ C、 $a \geq 1$ 且 $a \neq 5$ D、 $a \neq 5$

查看试题解析
7. 已知点 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (4 ， y_{3})$ 在抛物线 $y = - (x - 2)^{2} + 5$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
8. 函数 $y = a x^{2} + b x + c (a \neq 0)$ 中 $y$ 与自变量 $x$ 的部分对应值如下表：
$x$
$\dots$
$- 1$
$0$
$1$
$2$
$3$
$\dots$
$y$
     $\dots$
     $8$
     $3$
     $0$
     $- 1$
     $0$
     $\dots$
则当 $y > 8$ 时， $x$ 的取值范围是（）

A、 $- 1 < x < 5$ B、 $0 < x < 3$ C、 $x < - 1$ 或 $x > 5$ D、 $x < 0$ 或 $x > 3$

查看试题解析
9. 二次函数 $y = x^{2} - b x + b$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，抛物线 $y = m (x - 3)^{2} + k$ 与 $x$ 轴交于 $(a ， 0)$ ， $(b ， 0)$ 两点，其中 $a < b .$ 将此抛物线向上平移，与 $x$ 轴交于 $(c ， 0)$ ， $(d ， 0)$ 两点，其中 $c < d$ ，下面结论正确的是（）

A、当 $m > 0$ 时， $a + b = c + d$ ， $b - a > d - c$ B、当 $m > 0$ 时， $a + b > c + d$ ， $b - a = d - c$ C、当 $m < 0$ 时， $a + b = c + d$ ， $b - a > d - c$ D、当 $m < 0$ 时， $a + b > c + d$ ， $b - a < d - c$

查看试题解析

二、填空题（本大题共8小题，共16.0分）

11. 若关于 $x$ 的函数 $y = (a + 1) x^{2} - 2 x + 3$ 是二次函数，则 $a$ 的取值范围是．

查看试题解析
12. 若 $x = 2$ 是一元二次方程 $x^{2} + 3 x + k = 0$ 的一个根，则k的值为。

查看试题解析
13. 请你写出一个二次函数满足以下条件：
$①$ 开口向下；
$②$ 与 $y$ 轴交于点 $(0 ， - 3)$ ．

查看试题解析
14. 如图，直线 $y = m x + n$ 与抛物线 $y = x^{2} + b x + c$ 交于 $A$ ， $B$ 两点，其中点 $A (2 ， - 3)$ ，点 $B (5 ， 0)$ ，不等式 $x^{2} + b x + c < m x + n$ 的解集为．

查看试题解析
15. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ，且 $∠ O C D = 90 °$ ，若 $E$ 是 $B C$ 边的中点， $A C = 10$ ， $B D = 26$ ，则 $O E$ 的长为．

查看试题解析
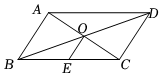16. 为响应国家号召打赢脱贫攻坚战，小明利用信息技术开了一家网络商店，将家乡的土特产销往全国．今年 $6$ 月份盈利 $12000$ 元， $8$ 月份盈利 $27000$ 元，求 $6$ 月份到 $8$ 月份盈利的月平均增长率．设 $6$ 月份到 $8$ 月份盈利的月平均增长率为 $x$ ，根据题意，可列方程为．

查看试题解析
17. 已知抛物线 $y = k x^{2} - 2 (k - 1) x + k + 1$ ，若抛物线关于 $y$ 轴对称，则 $k =$ ，此时抛物线关于 $x$ 轴对称的图象解析式为．

查看试题解析
18. 已知某函数的图象过 $A (2 ， - 1)$ ， $B (4 ， 1)$ 两点，下面有四个推断：
$①$ 若此函数的图象为直线，则此函数的图象经过 $(0 ， - 3)$ ；
$②$ 若此函数的图象为抛物线，且经过 $(1 ， - 0.5)$ ，则该抛物线开口向下；
$③$ 若此函数的解析式为 $y = a (x - h)^{2} + k (a \neq 0)$ ，且经过原点，则 $0 < h < 1$ ；
$④$ 若此函数的解析式为 $y = a (x - h)^{2} + k (a \neq 0)$ ，开口向下，且 $2 < h < 4$ ，则 $a$ 的范围是 $a < - \frac{1}{2}$ ．
所有合理推断的序号是．

查看试题解析

三、解答题（本大题共9小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）

19. 选择合适的方法解方程：

(1)、 $x^{2} - 4 = 0$ ；

(2)、 $x^{2} - 6 x + 8 = 0$ ．

查看试题解析
20. 已知二次函数 $y = x^{2} - 6 x + 5$ ．

(1)、求二次函数图象的顶点坐标；

(2)、在平面直角坐标系中，画出二次函数的图象；

(3)、当 $1 < x < 4$ 时，结合函数图象，直接写出 $y$ 的取值范围．

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + 2 x + c$ 的部分图象经过点 $A (0 ， - 3)$ ， $B (1 ， 0)$ ．

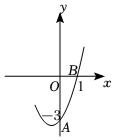(1)、求该抛物线的解析式；

(2)、结合函数图象，直接写出 $y < 0$ 时， $x$ 的取值范围；

(3)、将该抛物线向上平移个单位后，所得抛物线与 $x$ 轴只有一个公共点．

查看试题解析
22. 关于 $x$ 的一元二次方程 $x^{2} + 3 x + m = 0$ ．

(1)、若该方程无实数根，求 $m$ 的取值范围；

(2)、给 $m$ 取一个适当的值，使该方程有两个不同的实数根，并求出方程的两个根．

查看试题解析
23. 已知抛物线 $y = x^{2} + b x + c$ 与 $y$ 轴交于点 $C (0 ， 3)$ ，顶点为 $T$ ，与直线 $y = k x - 1$ 交于 $A$ ， $B$ 两点，其中点 $A$ 坐标为 $(1 ， 0)$ ．

(1)、求抛物线和直线解析式；

(2)、直接写出抛物线 $y = x^{2} + b x + c$ 关于 $x = - 1$ 对称的抛物线的解析式；

(3)、求 $△ A B T$ 的面积．

查看试题解析
24. 如图，一个圆形喷水池的中央竖直安装了一个柱形喷水装置 $O A$ ， $O A = \frac{1}{2} m$ ，从 $A$ 处向外喷出的水流在各个方向上沿形状相同的抛物线路径落下 $.$ 王丽芳同学根据题意在图中建立如图所示的坐标系，水流喷出的高度 $y (m)$ 与水平距离 $x (m)$ 之间的关系式是 $y = a x^{2} + b x + c (x > 0)$ ，已知水流的最高点到 $O A$ 的水平距离是 $\frac{1}{4} m$ ，最高点离水面是 $\frac{9}{16} m$ ．

(1)、求二次函数表达式；

(2)、若不计其他因素，水池的半径至少为多少米，才能使喷出的水流不至于落在池外？

查看试题解析
25. 已知二次函数 $y = a x^{2} - 2 a x - 2 (a > 0)$ ．

(1)、求该二次函数图象的对称轴；

(2)、当 $- 1 \leq x \leq 5$ 时，函数图象的最高点为 $M$ ，最低点为 $N$ ，点 $M$ 的纵坐标为 $\frac{11}{2}$ ，求点 $M$ 和点 $N$ 的坐标；

(3)、对于该二次函数图象上的两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，当 $t + 1 < x_{1} < t + 2$ ， $t + 3 < x_{2} < t + 4$ 时，均有 $y_{1} \neq y_{2}$ ，请结合图象，直接写出 $t$ 的取值范围．

查看试题解析
26. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点 $D$ 在 $B C$ 边上 $($ 不与点 $B$ ， $C$ 重合 $)$ ，将线段 $A D$ 绕点 $A$ 顺时针旋转 $90 °$ ，得到线段 $A E$ ，连接 $D E$ ．

(1)、根据题意补全图形，并证明： $∠ E A C = ∠ A D C$ ；

(2)、取 $D E$ 的中点 $F$ ，连接 $C F$ ，用等式表示线段 $C F$ 与 $B D$ 之间的数量关系，并证明．

查看试题解析
27. 对于平面图形 $G_{1}$ ， $G_{2}$ 和直线 $y = k x + b ($ 这里 $k$ ， $b$ 均为常数 $)$ ，若它们同时满足以下两个条件：
$a .$ 对 $G_{1}$ 上任意一点 $(p ， m)$ ，均有 $m \leq k p + b$ ；
$b .$ 对 $G_{2}$ 上任意一点 $(q ， n)$ ，均有 $n \geq k q + b$ ．
则称直线 $y = k x + b$ 是图形 $G_{1}$ ， $G_{2}$ 的“分界线”．
回答以下问题．

(1)、如图 $1$ 所示，在平面直角坐标系中有正方形 $A B C D$ 和三角形 $E F G .$ 例如：直线 $y = - x$ 是正方形 $A B C D$ 和三角形 $E F G$ 的一条“分界线”．
$(i)$ 在下列直线中，可以作为正方形 $A B C D$ 和三角形 $E F G$ 的“分界线”的是 ▲ $($ 填选项的标号 $)$ ；
$① y = 0$ ；
$② y = x$ ；
$③ y = 3 x$ ；
$④ y = - x - 1$ ．
$(i i)$ 若直线 $y = k x + 1$ 是正方形 $A B C D$ 和三角形 $E F G$ 的“分界线”，结合图形，求 $k$ 的取值范围．

(2)、如图 $2$ 所示，在平面直角坐标系中有抛物线 $M$ ： $y = - (x - t)^{2} + 2$ 和正方形 $H I J K$ ，正方形 $H I J K$ 的顶点 $H$ 的坐标为 $(t + 2 ， 0) .$ 若直线 $y = - 2 x - 2$ 是抛物线 $M$ 和正方形 $H I J K$ 的“分界线”，直接写出 $t$ 的取值范围．

查看试题解析

$x$	$\dots$	$- 1$	$0$	$1$	$2$	$3$	$\dots$
$y$	$\dots$	$8$	$3$	$0$	$- 1$	$0$	$\dots$