天津市西青区2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-11-15 类型：期中考试

进入出卷网下载

一、选择题（本大题共12小题，共36.0分，在每小题列出的选项中，选出符合题目的一项）

1. 下列方程中，属于一元二次方程的是（）

A、x²－3x＋2＝0 B、x²－xy＝2 C、x²＋ $\frac{1}{x}$ ＝2 D、2（x－1）＝x

查看试题解析
2. 抛物线y＝2（x－1）²＋6的顶点坐标是（）

A、（1，－6） B、（－1，－6） C、（1，6） D、（－1，6）

查看试题解析
3. 若x=2是关于x的一元二次方程x²-mx+8=0的一个解．则m的值是（　　）

A、6 B、5 C、2 D、-6

查看试题解析
4. 将抛物线y＝－3x²向左平移2个单位，再向下平移1个单位，所得抛物线为（）

A、y＝－3（x－2）²－1 B、y＝－3（x－2）²＋1 C、y＝－3（x＋2）²－1 D、y＝－3（x＋2）²＋1

查看试题解析
5. 对抛物线：y＝－x²＋2x－3而言，下列结论正确的是（）

A、与x轴有两个交点 B、开口向上 C、与y轴的交点坐标是（0，3） D、顶点坐标是（1，－2）

查看试题解析
6. 二次函数y＝ax²＋bx－1（a≠0）的图象经过点（1，1），则a＋b＋1的值是（）

A、－3 B、－1 C、2 D、3

查看试题解析
7. 用配方法解方程x²－2x－1＝0时，配方后得的方程为（）

A、（x＋1）²＝0 B、（x－1）²＝0 C、（x＋1）²＝2 D、（x－1）²＝2

查看试题解析
8. 关于x的一元二次方程kx²－6x＋1＝0有两个不相等的实数根，则k的取值范围是（）

A、k＞9 B、k＜9 C、0＜k＜9 D、k＜9且k≠0

查看试题解析
9. 如图，将等边三角形OAB放在平面直角坐标系中，A点坐标（1，0），将△OAB绕点O逆时针旋转60°，则旋转后点B的对应点 $B^{'}$ 的坐标为（）

A、 $(- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ B、 $(- 1 ， \frac{1}{2})$ C、 $(- \frac{3}{2} ， \frac{\sqrt{3}}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， \frac{1}{2})$

查看试题解析
10. 2020年，新型冠状病毒感染的肺炎疫情牵动着全国人民的心，雅礼中学某学生写了一份预防新型冠状病毒倡议书在微信朋友圈传播，规则为：将倡议书发表在自己的朋友圈，再邀请n个好友转发倡议书，每个好友转发倡议书又邀请n个互不相同的好友转发倡议书，以此类推，已知经过两轮传播后，共有931人参与了传播活动，则方程列为（）

A、（1＋n）²＝931 B、n（n－1）＝931 C、1＋n＋n²＝931 D、n＋n²＝931

查看试题解析
11. 如图所示是抛物线型的拱桥，当拱顶离水面2米时，水面宽4米，如果水面宽为 $2 \sqrt{6}$ 米，则水面下降（）米．

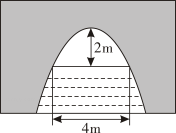A、1米 B、2米 C、3米 D、10米

查看试题解析
12.
已知二次函数y＝ax²+bx+c(a≠0)的图象如图所示，给出以下结论：① a+b+c＜0；② a－b+c＜0；③ b+2a＜0；④ abc＞0 。其中所有正确结论的序号是（　　）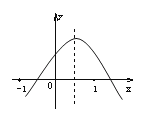

A、③④ B、②③ C、①④ D、①②③

查看试题解析

二、填空题（本大题共6小题，共18.0分）

13. 方程x²＝2的根是．

查看试题解析
14. 若正方形的边长为x ，面积为y ，则y与x之间的关系式为（x＞0）．

查看试题解析
15. 已知 $x_{1} 、 x_{2}$ 是一元二次方程x²＋2x－1＝0的两个实数根，则 $x_{1} + x_{2}$ 的值是．．

查看试题解析
16. 若抛物线y＝ax²＋bx＋c与x轴的两个交点坐标是（－1，0），（3，0），则此抛物线的对称轴是直线．

查看试题解析
17. 如图，当一喷灌架为一农田喷水时，喷灌架喷射出的水流可以近似地看成抛物线 $y = - \frac{1}{10} (x - 5)^{2} + 3.6$ ，则该喷灌架喷出的水可到达的最远距离OA＝米．

查看试题解析
18. 如图，点E在正方形 $A B C D$ 的边 $C D$ 上，将 $△ A D E$ 绕点A顺时针旋转90°到 $△ A B F$ 的位置，连接 $E F$ ，过点A作 $E F$ 的垂线，垂足为点H，与 $B C$ 交于点G，若 $B G = 3$ ， $C G = 2$ ，则 $C E$ 的长为．

查看试题解析

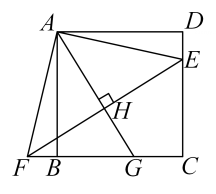
三、解答题（本大题共7小题，共66.0分，解答应写出文字说明，证明过程或演算步骤）

19. 用适当的方法解下列方程

(1)、（x＋3）²＝2x＋6；

(2)、x²＋5x＋7＝3x＋11

查看试题解析
20. 青山村种的水稻2007年平均每公顷产8000kg，2009年平均每公顷产9680kg，求该村水稻每公顷产量的年平均增长率．（注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答）
解题方案：
设该村水稻每公顷产量的年平均增长率为x ．

(1)、用含x的代数式表示：
①2008年种的水稻平均每公顷的产量为     ▲  ；
②2009年种的水稻平均每公顷的产量为     ▲  ；

(2)、根据题意，列出相应方程     ▲  ；

(3)、解这个方程，得     ▲  ；

(4)、检验：     ▲  ；

(5)、答：该村水稻每公顷产量的年平均增长率为     ▲  %．

查看试题解析
21. 某商场以每件220元的价格购进一批商品，当每件商品售价为280元时，每天可售出30件，为了迎接“618购物节”，扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每天就可以多售出3件．设每件商品降价x元．

(1)、商场日销售量增加件，每件商品盈利元（用含x的代数式表示）；

(2)、要使商场每天销售这种商品的利润达3600元，且更有利于减少库存，则每件商品应降价多少元？

查看试题解析
22. 如图，若要建一个矩形场地，场地的一面靠墙，墙长10m，另三边用篱笆围成，篱笆总长20m，设垂直于墙的一边为xm，矩形场地的面积为Sm²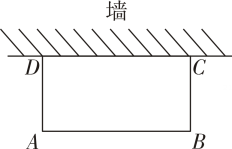

(1)、S与x的函数关系式为S＝ ▲ ，其中x的取值范围是 ▲ ；

(2)、当矩形场地的面积最大时，求矩形场地的长与宽，并求出矩形场地面积的最大值．

查看试题解析
23. 二次函数y＝ax²＋bx＋c（a ， b ， c为常数，a≠0）的自变量x与函数值y的部分对应值如表：
x
…
－2
0
2
4
6
…
y＝ax²＋bx＋c
…
0
6
m
n
0
…

(1)、该二次函数解析式为     ▲  ，m＝     ▲  ，n＝     ▲  ；

(2)、请在给出的平面直角坐标系中，画出二次函数y＝ax²＋bx＋c的图象；

(3)、根据图象直接写出下列问题：
①当x＝     ▲  时，y有最值     ▲  （填“大”或“小”）是     ▲  ．
②若该二次函数图象上有两点 $P_{1} (x_{1} ， y_{1})$ 和 $P_{2} (x_{2} ， y_{2})$ 满足 $2 < x_{1} < x_{2}$ ，则y₁     ▲  y₂（从符号＜，≤，≥，＞，＝中选择一个填空）
③当ax²＋bx＋c＞n时，x的取值范围是     ▲  ．
④当－2＜x＜4时，则y的取值范围是     ▲     ．

查看试题解析
24. 在平面直角坐标系中，O为原点，点A（3，0），点B（0，4），把△ABO绕点B逆时针旋转，得△ $A^{'} B O^{'}$ ，点A ， O旋转后的对应点为 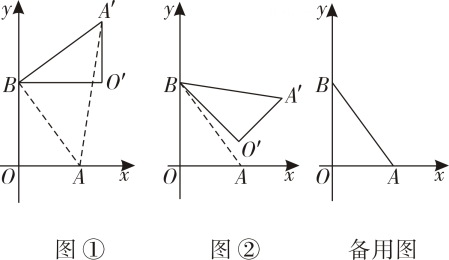$A^{'}$ ， $O^{'}$ ，记旋转角为 $α$ ．

(1)、如图①，若 $α$ ＝90°，求 $A A^{'}$ 的长；

(2)、如图②，若 $α$ ＝45°，求点 $O^{'}$ 的坐标．

查看试题解析
25. 在平面直角坐标系xOy中，关于x的二次函数y＝x²＋px＋q的图象过点（－1，0），（3，0）．

(1)、求这个二次函数的解折式；

(2)、求当－2≤x≤6时，y的最大值与最小值的差；

(3)、一次函数y＝（2－m）x＋2－m的图象与二次函数y＝x²＋px＋q图象交点的横坐标分别是a和b ，且a＜3＜b ，求m的取值范围．

查看试题解析

x	…	－2	0	2	4	6	…
y＝ax²＋bx＋c	…	0	6	m	n	0	…