河北省石家庄外国语教育集团2023-2024学年九年级上学期月考数学学科
试卷更新日期:2023-11-15 类型:月考试卷
一、选择题(本大题有16个小题,每小题3分, 共48分; 在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 如图,在中, , 则的值为( )
 A、 B、 C、 D、2. 如图,小明的一张书法练习纸,练习纸中的竖格线都平行,且相邻两条竖格线间的距离都相等,同一条直线上的三个点都在竖格线上,若线段 , 则线段的长为( )
A、 B、 C、 D、2. 如图,小明的一张书法练习纸,练习纸中的竖格线都平行,且相邻两条竖格线间的距离都相等,同一条直线上的三个点都在竖格线上,若线段 , 则线段的长为( ) A、6.4cm B、8cm C、9.6cm D、12.8cm3. 某厂现有300吨煤,这些煤能烧的天数与平均每天烧的吨数之间的函数关系是( )A、 B、 C、 D、4. 已知线段为成比例线段,其中 , 则等于( )A、1cm B、4cm C、9cm D、12cm5. 已知矩形中, , 下面四个矩形中与矩形相似的是( )A、
A、6.4cm B、8cm C、9.6cm D、12.8cm3. 某厂现有300吨煤,这些煤能烧的天数与平均每天烧的吨数之间的函数关系是( )A、 B、 C、 D、4. 已知线段为成比例线段,其中 , 则等于( )A、1cm B、4cm C、9cm D、12cm5. 已知矩形中, , 下面四个矩形中与矩形相似的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在高出海平面100米的悬崖顶处,观测海平面上一艘小船 , 并测得它的俯角为45°,则船与观测者之间的水平距离=( )
6. 如图,在高出海平面100米的悬崖顶处,观测海平面上一艘小船 , 并测得它的俯角为45°,则船与观测者之间的水平距离=( ) A、米 B、50米 C、米 D、100米7. 如图,在直角坐标平面内,点与原点的距离 , 线段与轴正半轴的夹角为 , 且 , 则点的坐标是( )
A、米 B、50米 C、米 D、100米7. 如图,在直角坐标平面内,点与原点的距离 , 线段与轴正半轴的夹角为 , 且 , 则点的坐标是( ) A、 B、 C、 D、8. 已知关于的方程, 有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、9. 如图,某同学拿着一把12cm长的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子恰好遮住电线杆,已知臂长60cm,则电线杆的高度是( )
A、 B、 C、 D、8. 已知关于的方程, 有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、9. 如图,某同学拿着一把12cm长的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子恰好遮住电线杆,已知臂长60cm,则电线杆的高度是( ) A、2.4m B、24m C、0.6m D、6m10. 老师设计了接力游戏,用合作的方式完成配方法解一元二次方程,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后解出方程.过程如图所示:
A、2.4m B、24m C、0.6m D、6m10. 老师设计了接力游戏,用合作的方式完成配方法解一元二次方程,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后解出方程.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A、只有甲 B、甲和乙 C、甲和丙 D、丙和丁11. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、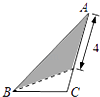 B、
B、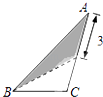 C、
C、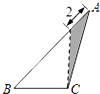 D、
D、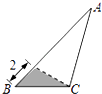 12. 杭州亚运会吉祥物深受大家喜爱,某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售 11.5万个,设该摆件销售量的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、13. 如图,若和的面积分别为 , , 则=( )
12. 杭州亚运会吉祥物深受大家喜爱,某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售 11.5万个,设该摆件销售量的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、13. 如图,若和的面积分别为 , , 则=( ) A、5:8 B、8:5 C、1:1 D、2:714. 如图, , 与的面积分别是和 , 与的周长分别是和 , 则一定成立的等式是( )
A、5:8 B、8:5 C、1:1 D、2:714. 如图, , 与的面积分别是和 , 与的周长分别是和 , 则一定成立的等式是( ) A、 B、 C、 D、15. 如图,岛位于岛的正西方,两岛间的距离为海里,由岛分别测得船位于南偏东60°和南偏西45°方向上,则船到岛的距离为( )
A、 B、 C、 D、15. 如图,岛位于岛的正西方,两岛间的距离为海里,由岛分别测得船位于南偏东60°和南偏西45°方向上,则船到岛的距离为( )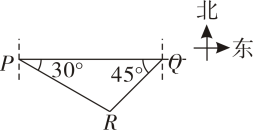 A、40海里 B、海里 C、海里 D、海里16. 对于题目“如图, 纸片四边形 , , 点是上一个动点,过点作直线 , 交AD(或其延长线)于点 , 以为折线,将四边形折叠,若重叠的部分的面积为4,确定满足条件的所有的长”,甲的结果是: , 乙的结果是: , 则( )
A、40海里 B、海里 C、海里 D、海里16. 对于题目“如图, 纸片四边形 , , 点是上一个动点,过点作直线 , 交AD(或其延长线)于点 , 以为折线,将四边形折叠,若重叠的部分的面积为4,确定满足条件的所有的长”,甲的结果是: , 乙的结果是: , 则( ) A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲 、乙的结果合在一起也不正确
A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲 、乙的结果合在一起也不正确二、填空题(本大题有3个小题,共 10分,17~18小题各3分,19题每空2分,把答案写在答题纸中相应的横线上)
-
17. 若 , 则=;18. 如图,河堤的横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是cm.
 19. 某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润增加2元,但一天产量减少5件.
19. 某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润增加2元,但一天产量减少5件.⑴若生产的是第三档的产品时,每件利润为元;
⑵若生产第档的产品一天的总利润为1120元,则该产品的质量档次为第档.
三、解答题(本大题有8个小题,共62分.解答应写出文字说明、证明过程或演算步骤)
-
20. 如图,已知是坐标原点,两点的坐标分别为 ,
 (1)、以点为位似中心,在轴左侧将放大为原来的两倍,画出图形;(2)、点的对应点的坐标是;点的对应点的坐标是;(3)、在上有一点 , 按(1)的方式得到的对应点的坐标是 .21.(1)、计算:(2)、 解方程:(3)、若是一元二次方程 的一个实数根,求 的值.22. 如图所示,延长平行四边形一边至点 , 连结交于点 , 若 .
(1)、以点为位似中心,在轴左侧将放大为原来的两倍,画出图形;(2)、点的对应点的坐标是;点的对应点的坐标是;(3)、在上有一点 , 按(1)的方式得到的对应点的坐标是 .21.(1)、计算:(2)、 解方程:(3)、若是一元二次方程 的一个实数根,求 的值.22. 如图所示,延长平行四边形一边至点 , 连结交于点 , 若 . (1)、求证:;(2)、若 , 则的长 .23. 如图,直角三角板如图所示在平面直角坐标系内,=30°,为坐标原点,作轴, , 若=30°.
(1)、求证:;(2)、若 , 则的长 .23. 如图,直角三角板如图所示在平面直角坐标系内,=30°,为坐标原点,作轴, , 若=30°. (1)、 点的坐标为;=;(2)、 求边所在直线的表达式;(3)、 直线自与直线重合的位置向下平移,当其平分三角形面积时,直接写出直线的表达式.24. 如图1,某款线上教学设备由底座,支撑臂 , 连杆 , 悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂 , , 固定 , 可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)、 点的坐标为;=;(2)、 求边所在直线的表达式;(3)、 直线自与直线重合的位置向下平移,当其平分三角形面积时,直接写出直线的表达式.24. 如图1,某款线上教学设备由底座,支撑臂 , 连杆 , 悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂 , , 固定 , 可通过调试悬臂与连杆的夹角提高拍摄效果.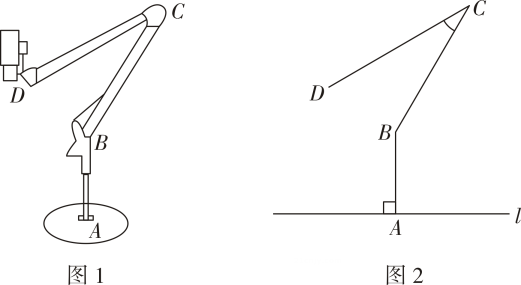 (1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)25. “绿水青山就是金山银山”,石家庄市在乡村振兴实施中,在山区发展养殖业,某农村合作社已经用篱笆圈定了如图所示的长方形养殖场 , 米,米,现计划在原有基础上进行扩建,雇佣两名工人同时沿着射线 , 射线方向继续匀速修建篱笆,两人工效相同,下表是方向的修建进度.
(1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)25. “绿水青山就是金山银山”,石家庄市在乡村振兴实施中,在山区发展养殖业,某农村合作社已经用篱笆圈定了如图所示的长方形养殖场 , 米,米,现计划在原有基础上进行扩建,雇佣两名工人同时沿着射线 , 射线方向继续匀速修建篱笆,两人工效相同,下表是方向的修建进度.时间/天
1
2
3
4
的长/米
310
320
330
340
 (1)、求的长度(米)与时间(天)的函数关系式;(2)、直接用含的关系式写出的长;(3)、两名工人工作若干天后,市政府安排工程队帮助合作社沿图2中的虚线修建好篱笆,最终将养殖场扩建成以为邻边的长方形,面积为 120000平方米,问两名工人各工作了几天?26. 如图1和图2,在中, , 直线 , 若自点出发以每秒1个单位长度的速度沿射线方向平移,同时点从点出发向点运动,速度是每秒2个单位长度,若直线分别与交于三点,连接 , 设运动时间为 .
(1)、求的长度(米)与时间(天)的函数关系式;(2)、直接用含的关系式写出的长;(3)、两名工人工作若干天后,市政府安排工程队帮助合作社沿图2中的虚线修建好篱笆,最终将养殖场扩建成以为邻边的长方形,面积为 120000平方米,问两名工人各工作了几天?26. 如图1和图2,在中, , 直线 , 若自点出发以每秒1个单位长度的速度沿射线方向平移,同时点从点出发向点运动,速度是每秒2个单位长度,若直线分别与交于三点,连接 , 设运动时间为 .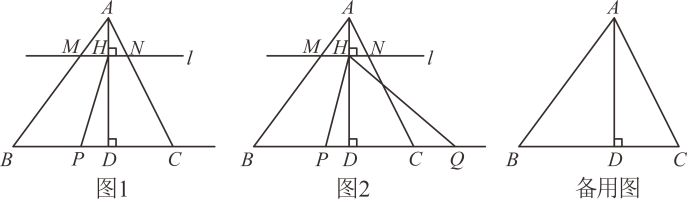 (1)、图中=;(2)、求当为何值时,;(3)、当四边形为平行四边形时,则=;(4)、在边或其延长线上取一点(点在的右侧),使得 , 直接写出:当 时,的值为多少?
(1)、图中=;(2)、求当为何值时,;(3)、当四边形为平行四边形时,则=;(4)、在边或其延长线上取一点(点在的右侧),使得 , 直接写出:当 时,的值为多少?