山西省晋中市灵石县2023-2024学年九年级上学期调研数学试卷（10月份）

试卷更新日期：2023-11-14 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

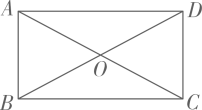
1. 下列方程中，是一元二次方程的是（）

A、 $x^{2} = 2 y - 3$ B、 $x^{2} = 9$ C、 $x^{2} + 3 x - 1 = x^{2} + 1$ D、 $\frac{2}{x^{2}} - 3 x - 15 = 0$

查看试题解析
2. 下列判断正确的是（）

A、对角线互相垂直的四边形是菱形 B、对角线相等的菱形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
3. 如图，在矩形 $A B C D$ 中， $A C$ ， $B D$ 相交于点 $O$ ，若 $△ A O B$ 的面积是 $4$ ，则矩形 $A B C D$ 的面积是（）

A、 $8$ B、 $12$ C、 $16$ D、 $20$

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 6 x + 5 = 0$ ，将其化成 $（ x + a ）^{2} = b$ 的形式，则变形正确的是（）

A、 $（ x + 3 ）^{2} = 4$ B、 $（ x - 3 ）^{2} = 4$ C、 $（ x - 6 ）^{2} = 31$ D、 $（ x + 6 ）^{2} = 11$

查看试题解析
5. 关于 $x$ 的一元二次方程 $3 x^{2} + 2 x + 1 = 0$ 的根的情况，下列判断正确的是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断

查看试题解析
6. 如图，菱形 $A B C D$ 的对角线交于点 $O$ ， $E$ 为 $A D$ 边的中点，如果菱形的周长为 $16$ ，那么 $O E$ 的长是（）

A、 $2$ B、 $3$ C、 $4$ D、 $6$

查看试题解析
7. 根据下列表格的对应值：
$x$
$6.17$
$6.18$
$6.19$
$6.20$
$a x^{2} + b x + c （ a ， b$ 、 $c$ 是常数，且 $a \neq 0 ）$
$- 0.03$
$- 0.01$
$0.02$
$0.04$
由此判断方程 $a x^{2} + b x + c = 0$ 的一个根 $x$ 的取值范围是（）

A、 $6 < x < 6.17$ B、 $6.17 < x < 6.18$ C、 $6.18 < x < 6.19$ D、 $6.19 < x < 9.20$

查看试题解析
8. 如图，在矩形ABCD中，O是BC的中点，∠AOD = 90°，若矩形ABCD的周长为30 cm，则AB的长为（　）

A、5 cm B、10 cm C、15 cm D、7.5 cm

查看试题解析
9. 顺次连接矩形 $A B C D$ 各边中点得到四边形 $E F G H$ ，它的形状是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $D$ 、 $E$ 、 $F$ 分别在边 $A B$ 、 $B C$ 、 $C A$ 上，且 $D E / / C A$ ， $D F / / B A .$ 下列四种说法，其中正确的有个（）
$①$ 四边形 $A E D F$ 是平行四边形； $②$ 如果 $∠ B A C = 90 °$ ，则四边形 $A E D F$ 是矩形； $③$ 如果 $A D$ 平分 $∠ B A C$ ，则四边形 $A E D F$ 是菱形； $④$ 如果 $A D ⊥ B C$ 且 $A B = A C$ ，则四边形 $A E D F$ 是菱形。

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

11. 方程 $x^{2} = x$ 的解是．

查看试题解析
12. 已知 $x = - 1$ 是关于 $x$ 的方程 $x^{2} + m x - n = 0$ 的一个根，则 $m + n$ 的值是 $=$ ．

查看试题解析
13. 如图，已知 $▱$ ABCD中对角线AC，BD相交于点O，请你添加一个适当的条件，使 $▱$ ABCD成为一个矩形．你添加的条件是．

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $A B = 5$ ，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，且 $A C = 6 . A E ⊥ C D$ 于点 $E$ ，则 $A E$ 的长是．

查看试题解析
15. 如图，正方形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $O$ ， $A E$ 平分 $∠ B A C$ 交 $B D$ 于点 $E$ ，若 $O A = 1$ ，则 $B E$ 的长为．

查看试题解析

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）

16. 解方程．

(1)、 $2 x^{2} - 5 x + 1 = 0 （$ 公式法 $）$ ．

(2)、 $4 （ 2 x - 3 ）^{2} = （ 3 x + 1 ）^{2}$ ．

查看试题解析
17.

(1)、解方程： $3 （ x - 2 ）^{2} = 2 - x$ ．

(2)、下面是小明解一元二次方程的过程，请认真阅读并完成相应的任务．
解： $2 x^{2} + 4 x - 8 = 0$
二次系数化为 $1$ ，得 $x^{2} + 2 x - 4 = 0 \dots$ 第一步
移项，得 $x^{2} + 2 x = 4 \dots$ 第二步
配方，得 $x^{2} + 2 x + 4 = 4 + 4$ ，即 $（ x + 2 ）^{2} = 8 \dots$ 第三步
由此，可得 $x + 2 = \pm 2 \sqrt{2} \dots$ 第四步
所以， $x_{1} = 2 + 2 \sqrt{2}$ ， $x_{2} = - 2 - 2 \sqrt{2} \dots$ 第五步
任务：
$①$ 上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程，体现的数学思想是    ▲         ，其中“配方法”所依据的一个数学公式是    ▲        ；
$②$ “第二步”变形的依据是    ▲        ；
$③$ 上面小明同学解题过程中，从第    ▲        步开始出现错误，请直接写出正确的解是    ▲        ；
$④$ 请你根据平时学习经验，就解一元二次方程时还需要注意的事项为其他同学提一条意见．

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $A C$ 是对角线，点 $E$ 是线段 $A C$ 延长线上的一点，在线段 $C A$ 的延长线上截取 $A F = C E$ ，连接 $D F$ ， $B F$ ， $D E$ ， $B E .$ 试判断四边形 $F B E D$ 的形状，并说明理由．

查看试题解析
19. $2023$ 亚洲花卉产业博览会于 $2023$ 年 $5$ 月 $10$ 至 $12$ 日，在中国进出口交易会展馆举办，为了迎接盛会的到来，组委会想利用一块长方形空地建了一个小型的惠民停车场，其布局如图所示，已知停车场的长为 $52 m$ ，宽为 $28 m$ ，阴影部分设计为停车位，其余部分是等宽的通道，已知停车位占地面积为 $640 m^{2} .$ 求通道的宽是多少米？

查看试题解析
20. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，垂足为 $D$ ， $A N$ 是 $△ A B C$ 外角 $∠ C A M$ 的平分线， $C E ⊥ A N$ ，垂足为 $E$ ，连接 $D E$ 交 $A C$ 于 $F$ ．

(1)、求证：四边形 $A D C E$ 为矩形．

(2)、线段 $D F$ 与 $A B$ 有怎样的位置关系和数量关系，并说明理由．

(3)、当 $△ A B C$ 满足什么条件时，四边形 $A D C E$ 是一个正方形？简述你的理由．

查看试题解析

21. 阅读材料：利用完全平方式，将多项式

x^{2} + b x + c

变形为

（ x + m ）^{2} + n

的形式，然后由

（ x + m ）^{2} \geq 0

就可以求出多项式

x^{2} + b x + c

的最小值．

例题：求 $x^{2} + 8 x + 21$ 的最小值

解： $x^{2} + 8 x + 21$

$= x^{2} + 2 x \cdot 4 + 4^{2} - 4^{2} + 21$

$= （ x + 4 ）^{2} + 5$ ．

无论 $x$ 取何值， $（ x + 4 ）^{2}$ 总是非负数，

即 $（ x + 4 ）^{2} \geq 0$ 所以 $（ x + 4 ）^{2} + 5 \geq 5$ ．

所以：当 $x = - 4$ 时， $x^{2} + 8 x + 21$ 有最小值，最小值为 $5$ ．

根据上述材料，解答下列问题：

(1)、填空：

x^{2} - 12 x +

= （ x -

）^{2}

；

(2)、将多项式

x^{2} + 16 x - 1

变形为

（ x + m ）^{2} + n

的形式，并求出

x^{2} + 16 x - 1

的最小值；

(3)、若一个长方形的长和宽分别为

（ 2 a + 3 ）

和

（ 3 a + 5 ）

，面积记为

S_{1}

，另一个长方形的长和宽分别为

5 a

和

（ a + 3 ）

，面积记为

S_{2}

，试比较

S_{1}

和

S_{2}

的大小，并说明理由．

查看试题解析

22. 综合与实践
问题情境：在综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动，请你解答各小组活动中产生的问题 $.$ 如图所示，在矩形 $A B C D$ 中， $A B = 4 c m$ ， $A D = 8 c m$ ，将矩形纸片进行折叠：

(1)、问题解决：如图 $1$ ，奋斗小组将该矩形沿对角线 $A C$ 折叠，点 $B$ 的对应点为点 $B'$ ，则 $D E =$ $c m$ ， $S_{△ A E C} =$ $c m^{2}$ ；

(2)、实践探究：如图 $2$ ，希望小组将矩形 $A B C D$ 沿着 $E F （$ 点 $E$ ， $F$ 分别在边 $A D$ ，边 $B C$ 上 $）$ 所在的直线折叠，点 $B$ 的对应点为点 $D$ ，连接 $B E$ ，
$①$ 试判断四边形 $B E D F$ 的形状，并说明理由；
$②$ 求折痕 $E F$ 的长．

查看试题解析
23. 综合与探究：
如图，直线 $l_{1}$ ： $y = \frac{3}{4} x$ 与直线 $l_{2}$ ： $y = - \frac{3}{4} x + 6$ 交于点 $A （ 4 ， m ）$ ，直线 $l_{2}$ 与 $x$ 轴交于点 $B （ n ， 0 ）$ ，点 $C$ 从点 $O$ 出发沿 $O B$ 向终点 $B$ 运动，速度为每秒 $1$ 个单位，同时点 $D$ 从点 $B$ 出发以同样的速度沿 $B O$ 向终点 $O$ 运动，作 $C M ⊥ x$ 轴，交折线 $O A - A B$ 于点 $M$ ，作 $D N ⊥ x$ 轴，交折线 $B A - A O$ 于点 $N$ ，设运动时间为 $t$ ．

(1)、求 $A$ ， $B$ 点的坐标；

(2)、在点 $C$ ，点 $D$ 运动过程中，
$①$ 当点 $M$ ， $N$ 分别在 $O A$ ， $A B$ 上时，求证四边形 $C M N D$ 是矩形；
$②$ 在点 $C$ ，点 $D$ 的整个运动过程中，当四边形 $C M N D$ 是正方形时，请你直接写出 $t$ 的值；

(3)、点 $P$ 是平面内一点，在点 $C$ 的运动过程中，问是否存在以点 $P$ ， $O$ ， $A$ ， $C$ 为顶点的四边形是菱形，若存在，请直接写出点 $P$ 的坐标，若不存在，请说明理由．

查看试题解析

$x$	$6.17$	$6.18$	$6.19$	$6.20$
$a x^{2} + b x + c （ a ， b$ 、 $c$ 是常数，且 $a \neq 0 ）$	$- 0.03$	$- 0.01$	$0.02$	$0.04$