浙江省金华市兰溪二中2023-2024学年八年级上学期数学10月考试试卷
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(共10小题,满分30分,每小题3分)
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 在△ABC中作AB边上的高,下列画法正确的是( )A、
2. 在△ABC中作AB边上的高,下列画法正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列语句是命题的是( )A、作直线AB的垂线 B、同旁内角互补 C、在线段AB上取点C D、垂线段最短吗?4. 若a、b、c为三角形的三边长,且a、b满足|a-2|+(b-1)2=0,则第三边长c的值可以是( )A、1 B、2 C、3 D、45. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=26. 不等式组的解在数轴上表示为( )A、
3. 下列语句是命题的是( )A、作直线AB的垂线 B、同旁内角互补 C、在线段AB上取点C D、垂线段最短吗?4. 若a、b、c为三角形的三边长,且a、b满足|a-2|+(b-1)2=0,则第三边长c的值可以是( )A、1 B、2 C、3 D、45. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=26. 不等式组的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 7. 如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是( )
7. 如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是( ) A、SSS B、SAS C、AAS D、ASA8. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
A、SSS B、SAS C、AAS D、ASA8. 如图,在中, , 是的高线,是的角平分线,则的度数是( )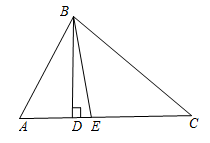 A、 B、 C、 D、9.
A、 B、 C、 D、9.在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+S2+S3+S4的值为( )
 A、6 B、5 C、4 D、310.
A、6 B、5 C、4 D、310.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
 A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23
A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23二、填空题(共6小题,满分24分)
-
11. 写出命题“对顶角相等.”的逆命题:如果 , 那么.它是一个命题.(填“真或假”)12. 已知三角形的三边长为3,5,x,则第三边x的取值范围是.13. 若关于x的不等式(a-1)x>1可化为x< , 则a的取值范围是.14. 等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为15. 已知关于x,y的方程组的解满足不等式组 , 则满足条件的m的整数值为.16. 如图,已知∠AOB=α,在射线OA、OB上分别取A、B1 , 使OA=OB1 , 连接AB1 , 在B1A、B1B上分别取点A1、B2 , 使B1B2=B1A1 , 连接A1B1…按此规律下去,记∠A1B1B2=θ1 , ∠A2B2B3=θ2 , …,∠AnBnBn+1=θn , 则:
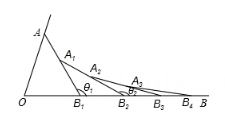 (1)、θ1=;(2)、θn=.
(1)、θ1=;(2)、θn=.三、解答题(共8小题,满分66分)
-
17. 解下列不等式(组):(1)、;(2)、.18. 解不等式组 , 并写出它的所有非负整数解.19. 如图,网格中每个小正方格的边长都为1,点A、B、C在小正方形的格点上.
 (1)、画出与△ABC关于直线l成轴对称的△A'B'C';(2)、求△ABC的面积.(3)、求BC边上的高.20. 如图,△ABC与△DCB中,AC与BD交于点E , 且∠A=∠D , AB=DC .
(1)、画出与△ABC关于直线l成轴对称的△A'B'C';(2)、求△ABC的面积.(3)、求BC边上的高.20. 如图,△ABC与△DCB中,AC与BD交于点E , 且∠A=∠D , AB=DC . (1)、求证:△ABE≌△DCE;
(1)、求证:△ABE≌△DCE;
(2)、当∠AEB=50°,求∠EBC的度数.
21. 如图,已知Rt△ABC中,∠C=90°.沿DE折叠,使点A与点B重合,折痕为DE. (1)、若DE=CE,求∠A的度数;(2)、若BC=6,AC=8,求CE的长.22. 在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?(3)、上面的哪种方案费用最低?按费用最低方案购买需要多少钱?23. 【问题解决】
(1)、若DE=CE,求∠A的度数;(2)、若BC=6,AC=8,求CE的长.22. 在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?(3)、上面的哪种方案费用最低?按费用最低方案购买需要多少钱?23. 【问题解决】如图1,点C为线段AB上一点,∠A=∠B=90°,AD=BC,BE=AC,连接CD、CE、DE.
 (1)、求证:△ACD≌△BEC.(2)、判断△CDE是哪种特殊三角形,并说明理由.(3)、【拓展延伸】
(1)、求证:△ACD≌△BEC.(2)、判断△CDE是哪种特殊三角形,并说明理由.(3)、【拓展延伸】如图2,点C为线段AB上一点,∠A=∠B=45°,CD⊥CE.当CD=CE时,求的值.
24. 如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒(t≠0). (1)、出发2秒后,求PQ的长;(2)、出发几秒钟后,直线PQ把△ABC的周长分成1:2的两部分;(3)、在点Q的运动过程中,是否存在时间t求能使△BCQ成为等腰三角形,如果有,请求出t,如果没有请说明理由.
(1)、出发2秒后,求PQ的长;(2)、出发几秒钟后,直线PQ把△ABC的周长分成1:2的两部分;(3)、在点Q的运动过程中,是否存在时间t求能使△BCQ成为等腰三角形,如果有,请求出t,如果没有请说明理由.