浙江省宁波市镇海区蛟川书院2023－2024学年七年级上学期数学期中试卷

试卷更新日期：2023-11-14 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分。共30分。请选出各题中唯一的正确选项。不选、多选、错选，均不给分）

1. 已知下列各数： $- 8 ， 2.57 ， 6 ， - \frac{1}{2} ， - 0.25 ， 1 \frac{2}{3} ， 0$ ，其中负有理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列式子中，正确的是（）

A、 $- | - 3 | = - (- 3)$ B、 $- \frac{3}{2} < - 1$ C、 $0 < - \frac{2}{3}$ D、 $- \frac{1}{5} > 1 - 2 ∣$

查看试题解析
3. 2023年中秋国庆假期恰逢“杭州亚运会”加持，浙江全省旅游接待游客总量创历史同期新高.全省共接待游客约43700000人次，将数据43700000用科学记数法表示应为（）

A、 $4.37 \times 1 0^{7}$ B、 $43.7 \times 1 0^{6}$ C、 $4.37 \times 1 0^{8}$ D、 $0.437 \times 1 0^{8}$

查看试题解析
4. 代数式 $x - y^{2}$ 的意义为（）

A、 $x$ 与 $y$ 的差的平方 B、 $x$ 与 $y$ 的平方的差 C、 $x$ 的平方与 $y$ 的差 D、 $x$ 的平方与 $y$ 的平方的差

查看试题解析
5. 下列各组中的两项属于同类项的是（）

A、 $- 4 x^{2} y$ 与 $\frac{2}{3} x^{2} y$ B、2abc与2ab C、 $- \frac{3}{x}$ 与 $- 3 x$ D、 $0.5 a^{2} c$ 与 $0.5 a^{2} b$

查看试题解析
6. 下列说法正确的是（）

A、代数式 $- \frac{x y^{2}}{5}$ 不是整式 B、单项式 $x$ 的系数为0 C、单项式 $- 2 π x y z^{2}$ 的次数为5 D、多项式 $a^{2} - 2 b$ 的次数为2

查看试题解析
7. 下列各式是一元一次方程的是（）

A、 $2 x = 5 + 3 y$ B、 $y^{2} = y + 4$ C、 $3 x + 2 = 1 - x$ D、 $\frac{1}{x} = 2$

查看试题解析
8. 下列说法正确的是（）

A、如果 $a c = b c$ ，那么 $a = b$ B、如果 $a = b$ ，那么 $a + 1 = b - 1$ C、如果 $a = b$ ，那么 $a c = b c$ D、如果 $a^{2} = b^{2}$ ，那么 $a = b$

查看试题解析
9. 有理数a，b，c在数轴上的对应点的位置如图所示.若 $| a | > | b | ， | c | > | b |$ ，则下列络论不一定成立的是（）

A、 $a < 0$ B、 $c > 0$ C、 $a + b < 0$ D、 $a + c < 0$

查看试题解析
10. 如图，7张全等的小长方形纸片（既不重叠也无空隙）放置于矩形ABCD中，设小长方形的长为a ，宽为b（a＞b），若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（　　）

A、 $a$ B、 $b$ C、 $a + b$ D、 $a - b$

查看试题解析

二、填空题(本题有8小题，每小题3分，共24分)

11. 如果温度上升 $3^{°} C$ ，记作 $+ 3^{°} C$ ，那么温度下降 $2^{°} C$ 记作℃.

查看试题解析
12. -3的倒数是。

查看试题解析
13. 已知关于 $x$ 的方程 $2 x + m - 8 = 0$ 的解是 $x = 3$ ，则 $m$ 的值为.

查看试题解析
14. 已知a，b满足 $| a + 3 | + (b - 2)^{2} = 0$ ，则 $(a + b)^{2003}$ 的值是.

查看试题解析
15. 某市出租车3千米以内收费8元，之后每增加1千米加收1.2元，某人乘出租车行驶了 $m (m > 3)$ 千米，则应付费元.(用含 $m$ 的代数式表示)

查看试题解析
16. 有理数 $a ， b ， c$ 在数轴上的对应点的位置如图所示，则 $| a - c | - | a - b | - | b - c |$ 的化简结果为.

查看试题解析
17. 已知 $a ， b ， c$ 是满足 $a + b + c = 2$ 的三个不同的整数，整数 $m$ 满足 $(a + m) (b + m) (c + m) = 25$ ，则 $m$ 的值为.

查看试题解析
18. 用若干根长为1的火柴恰好可以拼成如图1所示的47个边长为1的正方形，若将这些火柴按照如图2所示的方式拼，则可以拼出个边长为1的正方形.

查看试题解析

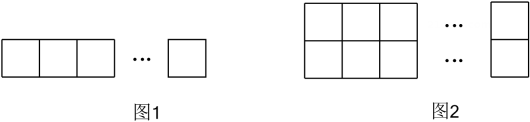
三、解答题（本题有6小题，第19题9分，第20题6分，第21题6分，第22题6分，第23题8分，第24题11分,共46分）

19. 计算：

(1)、 $- 32 - (+ 11) + (- 9) - (- 12)$

(2)、 $(- \frac{1}{6} - \frac{5}{12} + \frac{2}{3}) \times (- 72)$

(3)、 $- 1^{2023} - | \frac{1}{2} - 1 | \div 3 \times [2 - (- 3)^{2}]$

查看试题解析
20. 已知 $A = 3 x^{2} - x + 2 y - 4 x y ， B = 2 x^{2} - 3 x - y + x y$ .

(1)、化简 $2 A - 3 B$ .

(2)、当 $y$ 取何值时， $2 A - 3 B$ 的值与 $x$ 的取值无关.

查看试题解析
21. 解方程：

(1)、 $3 (20 - y) = 6 y - 4 (y - 11)$

(2)、 $\frac{0.4 x + 3}{0.2} - 2 = \frac{0.45 - x}{0.3}$

查看试题解析
22. 某水果店以每箱90元的价格从水果批发市场购进20箱樱桃，若以每箱净重5千克为标准，超过的千克数记为正数，不足的千克数记为负数，称重的记录如表：
与标准重量的差值(单位：千克)
-0.5
-0.25
0
0.2
0.25
0.5
箱数
2
2
4
5
n
3

(1)、求 $n$ 的值及这20箱樱桃的总重量；

(2)、该水果店第一天以每千克25元的价格销售了这批樱桃的70%，第二天因为害怕剩余樱桃腐烂，决定降价把剩余的樱桃以第一天零售价的60%全部售出．水果店在销售这批樱桃过程中是盈利还是亏损，盈利或亏损多少元?

查看试题解析
23. 用“ $P$ ”定义一种新运算：对于任意有理数 $x$ 和 $y ， x P y = a^{2} x^{2} - 2 a y + 1$ ( $a$ 为常数).例如： $1 P 2 = a^{2} \times 1^{2} - 2 a \times 2 + 1 = a^{2} - 4 a + 1$ .

(1)、当 $a = 1$ 时，求 $2 P (- 3)$ 的值.

(2)、若(-2)P2的值比 $2 P (- 2)$ 的值大2，求 $a$ 的值.

(3)、若 $(- 2) P 2$ 的值为5，求 $(- 4) P 8$ 的值.

查看试题解析
24. 如图，数轴上有A，B两点，A，B之间距离为15，原点 $O$ 在A，B之间， $O$ 到 $A$ 的距离是 $O$ 到 $B$ 的距离的两倍.

(1)、点 $A$ 表示的数为，点 $B$ 表示的数为；

(2)、点A、点 $B$ 和点 $P$ (点 $P$ 初始位置在原点 $O$ )同时向左运动，它们的速度分别为1，2，2个单位长度每秒，则经过多少秒，点 $P$ 到点 $A$ 与点 $B$ 的距离相等?

(3)、点 $B$ 沿着数轴移动，每次只允许移动1个单位长度，经过6次移动后，点 $B$ 与原点 $O$ 相距1个单位长度.满足条件的点 $B$ .的移动方法共有多少种?

(4)、点 $A$ 和点 $B$ 同时沿着数轴移动，两点每次均只允许移动1个单位长度.请判断点 $A$ 和点 $B$ 经过相同次数的移动后，能否同时到达原点 $O$ ?如果能，请给出点 $A$ 和点 $B$ 各自的移动方法；如果不能，请说明理由.

查看试题解析

与标准重量的差值(单位：千克)	-0.5	-0.25	0	0.2	0.25	0.5
箱数	2	2	4	5	n	3