山东省东营市利津县2023-2024学年七年级上学期第一次月考数学试卷(五四学制)
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列长度的三条线段能组成三角形的是( )A、3,3,6 B、3,5,10 C、4,6,9 D、4,5,92. 画中边上的高,下列画法中正确的是( )A、
 边上的高
B、
边上的高
B、 边上的高
C、
边上的高
C、 边上的高
D、
边上的高
D、 边上的高
3. 如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是( )
边上的高
3. 如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是( )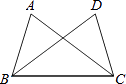 A、∠A=∠D B、∠ABD=∠DCA C、∠ACB=∠DBC D、∠ABC=∠DCB4. 已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )A、2cm B、3cm C、6cm D、13cm5. 如图, , , 垂足分别为、 , , 且 , 那么≌的理由是( )
A、∠A=∠D B、∠ABD=∠DCA C、∠ACB=∠DBC D、∠ABC=∠DCB4. 已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )A、2cm B、3cm C、6cm D、13cm5. 如图, , , 垂足分别为、 , , 且 , 那么≌的理由是( ) A、 B、 C、 D、6. 如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )
A、 B、 C、 D、6. 如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )①以点 为圆心,以 为半径画弧,以点 为圆心,以 为半径画弧,两弧交于 点;②作线段 等于 ;③连接 , ,则 就是所求作图形.
A、①②③ B、③②① C、②①③ D、②③①8. 如图,在中,已知点、分别为边、、上的中点,且 , 则的值为( ) A、 B、 C、 D、9. 如图,中,为的角平分线,为的高,与交于点 , , , 那么( )
A、 B、 C、 D、9. 如图,中,为的角平分线,为的高,与交于点 , , , 那么( ) A、 B、 C、 D、10. 如图,已知 , , 下列结论:
A、 B、 C、 D、10. 如图,已知 , , 下列结论:
;; , 其中正确的结论有( )
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,共32.0分)
-
11. 我们用如图的方法(斜钉上一块木条)来修理一条摇晃的凳子的数学原理是利用三角形的.
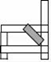 12. 如图,要测量水池宽 , 可从点出发在地面上画一条线段 , 使 , 再从点观测,在的延长线上测得一点 , 使 , 这时量得 , 则水池宽的长度是
12. 如图,要测量水池宽 , 可从点出发在地面上画一条线段 , 使 , 再从点观测,在的延长线上测得一点 , 使 , 这时量得 , 则水池宽的长度是 13. △ABC中,当∠A:∠B:∠C=1:2:3时,这个三角形是 三角形.(填“锐角”“直角”“钝角”)14. 如图, , , 且 , , 则的长为 .
13. △ABC中,当∠A:∠B:∠C=1:2:3时,这个三角形是 三角形.(填“锐角”“直角”“钝角”)14. 如图, , , 且 , , 则的长为 . 15. 把一张长方形纸片按如图所示的方式折叠,、为折痕,折叠后的点落在处,点落在处,点落在处,且、、在同一条直线上,那么的度数是 .
15. 把一张长方形纸片按如图所示的方式折叠,、为折痕,折叠后的点落在处,点落在处,点落在处,且、、在同一条直线上,那么的度数是 . 16. 如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为.
16. 如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为. 17. 如图,是一个任意角,在边 , 上分别取 , 移动角尺,使角尺两边相同的刻度分别与 , 重合,过角尺顶点的射线是的平分线 , 由做法得到三角形全等的判定方法是 .
17. 如图,是一个任意角,在边 , 上分别取 , 移动角尺,使角尺两边相同的刻度分别与 , 重合,过角尺顶点的射线是的平分线 , 由做法得到三角形全等的判定方法是 . 18. 如图, , 于 , 于 , 且 , 点从向运动,每分钟走 , 点从向运动, , 两点同时出发,点每分钟走时与全等.
18. 如图, , 于 , 于 , 且 , 点从向运动,每分钟走 , 点从向运动, , 两点同时出发,点每分钟走时与全等.
三、解答题(本大题共6小题,共58.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 如图,AC平分∠BAD , CB⊥AB , CD⊥AD , 垂足分别为B , D .
求证:△ABC≌△ADC .
 20. 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
20. 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE. 21. 如图,点 , , , 在同一直线上, , , , 请问吗?为什么?
21. 如图,点 , , , 在同一直线上, , , , 请问吗?为什么?


