四川省成都市青羊区重点中学2023-2024学年九年级上学期月考数学试卷(10月)
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(本大题共8小题,共32分)
-
1. 下列方程中是一元二次方程的是( )A、2x+1=0 B、y2+x=1 C、x2+1=0 D、2. 小强同学从 , , , , , 这六个数中任选一个数,满足不等式 的概率是( )A、 B、 C、 D、3. 若关于 的方程 有实数根,则实数 的取值范围是( )A、 B、 C、 D、 且4. 在数学活动课上,为探究四边形瓷砖是否为菱形,以下拟定的测量方案,正确的是( )A、测量一组对边是否平行且相等 B、测量四个内角是否相等 C、测量两条对角线是否互相垂直 D、测量四条边是否相等5. 如图,在平面直角坐标系中,点A的坐标为 , 以为一边作正方形 , 则点B的坐标为( )
 A、 B、 C、或 D、或6. 某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )
A、 B、 C、或 D、或6. 某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )次数
100
200
300
400
500
600
700
800
900
1000
频率
0.60
0.30
0.50
0.36
0.42
0.38
0.41
0.39
0.40
0.40
A、掷一个质地均匀的骰子,向上的面点数是“6” B、掷一枚一元的硬币,正面朝上 C、不透明的袋子里有2个红球和3个黄球,除颜色外都相同,从中任取一球是红球 D、三张扑克牌,分别是3,5,5,背面朝上洗匀后,随机抽出一张是57. 如图,矩形的两对角线相交于点 , , , 则矩形的面积为( )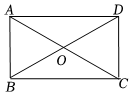 A、 B、 C、 D、8. 如图,在正方形外取一点 , 连接 , , 过点作的垂线交于点若 , , 则点到直线的距离为( )
A、 B、 C、 D、8. 如图,在正方形外取一点 , 连接 , , 过点作的垂线交于点若 , , 则点到直线的距离为( )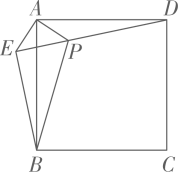 A、 B、 C、 D、
A、 B、 C、 D、二、非选择题(共118分)
-
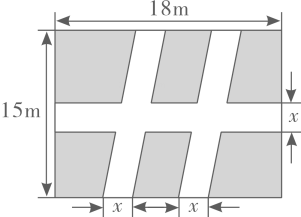
9. 某工厂一月份生产机器100台,计划二、三月份共生产机器250台,设二、三月份的平均增长率为x,则根据题意列出方程是 .10. 如图所示,某市世纪广场有一块长方形绿地长18m,宽15m,在绿地中开辟三条道路后,剩余绿地的面积为224m2 , 则图中x的值为 .
 11. 已知:m、n是方程的两根,则 .12. 一个菱形的周长是 , 一条对角线长 , 则这个菱形另外一条对角线的长度为 ,菱形的面积为 .13. 计算题(1)、;(2)、;(3)、;(4)、 .14. 已知关于的一元二次方程 .(1)、试证:无论取任何实数,方程都有两个不相等的实数根;(2)、设 , 为方程的两个实数根,且 , 求的值.15. 如图,矩形中,对角线 , 交于点 , 过点作的平行线,过点作的平行线,这两条平行线交于点 .
11. 已知:m、n是方程的两根,则 .12. 一个菱形的周长是 , 一条对角线长 , 则这个菱形另外一条对角线的长度为 ,菱形的面积为 .13. 计算题(1)、;(2)、;(3)、;(4)、 .14. 已知关于的一元二次方程 .(1)、试证:无论取任何实数,方程都有两个不相等的实数根;(2)、设 , 为方程的两个实数根,且 , 求的值.15. 如图,矩形中,对角线 , 交于点 , 过点作的平行线,过点作的平行线,这两条平行线交于点 .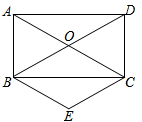 (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.16. 2023年杭州亚运会吉祥物一开售,就深受大家的喜爱,某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售,经统计,4月份的销售量为256件,6月份的销售量为400件.(1)、求该款吉祥物4月份到6月份销售量的月平均增长率.(2)、从7月份起,商场决定采用降价促销的方式回馈顾客.经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?17. 年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会.目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如图两幅不完整的统计图.
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.16. 2023年杭州亚运会吉祥物一开售,就深受大家的喜爱,某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售,经统计,4月份的销售量为256件,6月份的销售量为400件.(1)、求该款吉祥物4月份到6月份销售量的月平均增长率.(2)、从7月份起,商场决定采用降价促销的方式回馈顾客.经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?17. 年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会.目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如图两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、这次被调查的同学共有人;(2)、扇形统计图中“篮球”对应的扇形圆心角的度数为;(3)、现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.18. 如图,在平面直角坐标系中,点为坐标原点,直线分别交轴、轴于两点, , 且、的长分别是一元二次方程的两根. (1)、求直线的解析式;(2)、点从点出发沿射线方向运动,运动的速度为每秒个单位,设的面积 , 点运动的时间为 , 写出与的函数关系式,并直接写出自变量的取值范围;(3)、点是轴上的点,点是第一象限内的点,若以、、、为顶点的四边形是菱形请求出点的坐标.19. 若关于的方程是一元二次方程,则 .20. 已知 , 是方程的两个实数根,则的值为 .21. 有三张正面分别标有数字 , , 的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为 , 则使关于的不等式组的解集中有且只有个非负整数的概率为 .22. 对于两个不相等的实数、 , 我们规定符号表示、中的较大值,如: , 按照这个规定,方程的解为 .23. 如图,在平面直角坐标系中,已知矩形 , , 点为轴上的一个动点,以为边在右侧作等边 , 连接 , 则的最小值为 .
(1)、求直线的解析式;(2)、点从点出发沿射线方向运动,运动的速度为每秒个单位,设的面积 , 点运动的时间为 , 写出与的函数关系式,并直接写出自变量的取值范围;(3)、点是轴上的点,点是第一象限内的点,若以、、、为顶点的四边形是菱形请求出点的坐标.19. 若关于的方程是一元二次方程,则 .20. 已知 , 是方程的两个实数根,则的值为 .21. 有三张正面分别标有数字 , , 的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为 , 则使关于的不等式组的解集中有且只有个非负整数的概率为 .22. 对于两个不相等的实数、 , 我们规定符号表示、中的较大值,如: , 按照这个规定,方程的解为 .23. 如图,在平面直角坐标系中,已知矩形 , , 点为轴上的一个动点,以为边在右侧作等边 , 连接 , 则的最小值为 .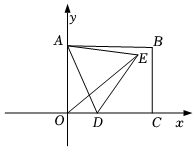 24. 如图,已知直线交轴于点 , 交轴于点 , , 的长是一元二次方程的两个根,设点的坐标为 , 的面积为 .
24. 如图,已知直线交轴于点 , 交轴于点 , , 的长是一元二次方程的两个根,设点的坐标为 , 的面积为 .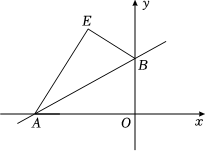 (1)、求直线的解析式;(2)、求与的函数关系式,并写出自变量的取值范围;(3)、若点在直线的上方, , 求出点的坐标.25. “抖音”平台爆红网络,某电商在“抖音”上直播带货,已知该产品的进货价为元件,为吸引流量,该电商在直播中承诺自家商品价格永远不会超过元件,根据一个月的市场调研,商家发现当售价为元件时,日销售量为件,售价每降低元,日销售量增加件.(1)、当销售量为件时,产品售价为 元件;(2)、直接写出日销售量件与售价元件的函数关系式;(3)、该产品的售价每件应定为多少,电商每天可盈利元?26. 如图 , 在坐标系中的 , 点、在轴,点在轴,且 , , , 是的中点.
(1)、求直线的解析式;(2)、求与的函数关系式,并写出自变量的取值范围;(3)、若点在直线的上方, , 求出点的坐标.25. “抖音”平台爆红网络,某电商在“抖音”上直播带货,已知该产品的进货价为元件,为吸引流量,该电商在直播中承诺自家商品价格永远不会超过元件,根据一个月的市场调研,商家发现当售价为元件时,日销售量为件,售价每降低元,日销售量增加件.(1)、当销售量为件时,产品售价为 元件;(2)、直接写出日销售量件与售价元件的函数关系式;(3)、该产品的售价每件应定为多少,电商每天可盈利元?26. 如图 , 在坐标系中的 , 点、在轴,点在轴,且 , , , 是的中点.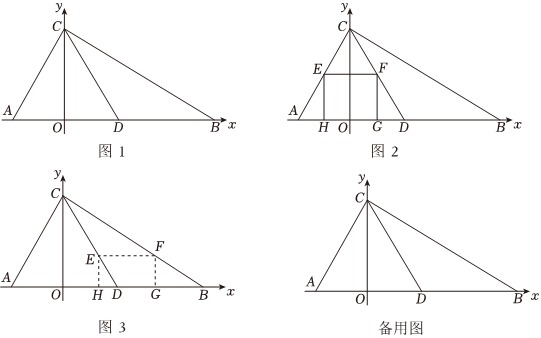 (1)、求直线的表达式;(2)、如图 , 若、分别是边 , 的中点,矩形的顶点都在的边上,若 , , 将矩形沿射线向右平移,设矩形移动的距离为 , 矩形与重叠部分的面积为 , 当时,请直接写出平移距离的值;(3)、如图 , 在的条件下,在矩形平移过程中,当点在边上时停止平移,再将矩形绕点按顺时针方向旋转,当点落在直线上时,此时矩形记作 , 由向轴作垂线,垂足为 , 请计算的值.
(1)、求直线的表达式;(2)、如图 , 若、分别是边 , 的中点,矩形的顶点都在的边上,若 , , 将矩形沿射线向右平移,设矩形移动的距离为 , 矩形与重叠部分的面积为 , 当时,请直接写出平移距离的值;(3)、如图 , 在的条件下,在矩形平移过程中,当点在边上时停止平移,再将矩形绕点按顺时针方向旋转,当点落在直线上时,此时矩形记作 , 由向轴作垂线,垂足为 , 请计算的值.