河北省沧州市东光县五校联考2023-2024学年九年级上学期月考数学试卷(10月)
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 在下列各点中,抛物线经过点( )A、 B、 C、 D、3. 解一元二次方程 , 最适用的方法是( )A、配方法 B、公式法 C、因式分解法 D、直接开方法4. 要由抛物线得到抛物线 , 则抛物线必须( )A、向左平移个单位,再向下平移个单位 B、向右平移个单位,再向上平移个单位 C、向右平移个单位,再向下平移个单位 D、向左平移个单位,再向上平移个单位5. 已知是关于的一元二次方程的一个根,则的值是( )A、 B、 C、 D、6. 关于二次函数的图象,下列结论正确的是( )A、开口向下 B、对称轴是直线 C、顶点纵坐标是 D、当时,函数值随值的增大而增大7. 若关于x的一元二次方程 的两个实数根分别为 ,那么抛物线 的对称轴为直线( )A、 B、 C、 D、8. 如果方程是关于的一元二次方程,那么的值为( )A、 B、 C、 D、都不对9. 如图,一次函数与二次函数的图象相交于 , 两点,则关于的不等式的解集为( )
 A、 B、 C、 D、或10. 一元二次方程的解的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定11. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛28场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、912. 小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为 , 其中是实心球飞行的高度,是实心球飞行的水平距离,已知该同学出手点的坐标为 , 则实心球飞行的水平距离的长度为( )
A、 B、 C、 D、或10. 一元二次方程的解的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定11. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛28场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、912. 小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为 , 其中是实心球飞行的高度,是实心球飞行的水平距离,已知该同学出手点的坐标为 , 则实心球飞行的水平距离的长度为( ) A、 B、 C、 D、13. 已知一元二次方程的两根分别为 , , 则的值为( )A、 B、 C、 D、14. 如图所示是二次函数的图象,以下结论:;;的两个根是 , ; , 其中正确的是( )
A、 B、 C、 D、13. 已知一元二次方程的两根分别为 , , 则的值为( )A、 B、 C、 D、14. 如图所示是二次函数的图象,以下结论:;;的两个根是 , ; , 其中正确的是( ) A、 B、 C、 D、15. 如图,在一块宽为 , 长为的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余阴影部分的面积为 , 问小路的宽应是多少?设小路的宽为 , 根据题意得( )
A、 B、 C、 D、15. 如图,在一块宽为 , 长为的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余阴影部分的面积为 , 问小路的宽应是多少?设小路的宽为 , 根据题意得( )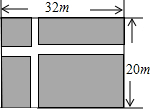 A、 B、 C、 D、以上都不正确16. 已知抛物线和直线在同一坐标系内的图象如图,其中正确的是( )A、
A、 B、 C、 D、以上都不正确16. 已知抛物线和直线在同一坐标系内的图象如图,其中正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共4小题,共12.0分)
-
17. 将一元二次方程化为一般形式后二次项系数为3,则一次项系数为.18. 点 , 在抛物线上,则 填“”、“”或“=” .19. 设为一元二次方程的一个实数根,则 .20. 如图,抛物线的对称轴为 , 点是抛物线与轴的一个交点,若点的坐标为 , 则关于的一元二次方程的解为 .

三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 用适当的方法解下列一元二次方程:(1)、;(2)、;(3)、;(4)、 .22. 已知、是关于的一元二次方程的两实根.(1)、则;1;(2)、若 , 求的值.23. 已知二次函数 的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
 (1)、求点A、B、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;(2)、设一次函数 的图象经过B、C两点,请直接写出满足 的x的取值范围.24. 如图,抛物线的顶点为 , 与轴交于 , 两点.
(1)、求点A、B、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;(2)、设一次函数 的图象经过B、C两点,请直接写出满足 的x的取值范围.24. 如图,抛物线的顶点为 , 与轴交于 , 两点.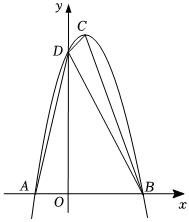 (1)、求抛物线的解析式;(2)、抛物线与轴的交点为 , 求 .25. 如图,利用一面墙墙长米 , 用总长度米的篱笆图中实线部分围成一个矩形鸡舍 , 且中间共留两个米的小门,设篱笆长为米.
(1)、求抛物线的解析式;(2)、抛物线与轴的交点为 , 求 .25. 如图,利用一面墙墙长米 , 用总长度米的篱笆图中实线部分围成一个矩形鸡舍 , 且中间共留两个米的小门,设篱笆长为米. (1)、米.用含的代数式表示(2)、若矩形鸡舍面积为平方米,求篱笆的长.(3)、矩形鸡舍面积是否有可能达到平方米?若有可能,求出相应的值;若不可能,则说明理由.26. 水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少元,发现原来买这种水果千克的钱,现在可买千克.
(1)、米.用含的代数式表示(2)、若矩形鸡舍面积为平方米,求篱笆的长.(3)、矩形鸡舍面积是否有可能达到平方米?若有可能,求出相应的值;若不可能,则说明理由.26. 水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少元,发现原来买这种水果千克的钱,现在可买千克. (1)、现在实际购进这种水果每千克多少元?(2)、王阿姨准备购进这种水果销售,若这种水果的销售量千克与销售单价元千克满足如图所示的一次函数关系.
(1)、现在实际购进这种水果每千克多少元?(2)、王阿姨准备购进这种水果销售,若这种水果的销售量千克与销售单价元千克满足如图所示的一次函数关系.求与之间的函数关系式;
请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?利润销售收入进货金额
27. 某“”景区决定在“”劳动节期间推出优惠套餐,预售“亲子两人游”套票和“家庭三人行”套票,预售中的“家庭三人行”套票的价格是“亲子两人游”套票的倍.(1)、若“亲子两人游”套票的预售额为元,“家庭三人行”套票的预售额为元,且“亲子两人游”的销售量比“家庭三人行”的套票多套,求“亲子两人游“套票的价格.(2)、套票在出售当天计划推出“亲子两人游”套票张,“家庭三人行”套票张,由于预售的火爆,景区决定将“亲子两人行”套票的价格在中价格的基础上增加元,而“家庭三人行”套票在中“家庭三人行”套票票价上增加了元,结果“亲子两人游”套票的销量比计划少套,“家庭三人行”套票的销售量与计划保持一致,最终实际销售额和计划销售额相同,求的值.