山东省德州市九中2023-2024学年八年级上学期月考数学试卷(10月)
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(本大题共12小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 以下数据分别是根小木棒的长度.用这根小木棒的长度为边不能搭成三角形的是( )A、 , , B、 , , C、 , , D、 , ,2. 如图,四个图形中,线段是的高的图是( )A、
 B、
B、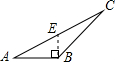 C、
C、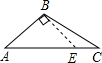 D、
D、 3. 具备下列条件的 , 不是直角三角形的是( )A、 B、 C、:::: D、4. 下列说法不正确的是( )A、多边形的内角和随多边形边数的增加而增加 B、多边形的外角和等于 C、若一个多边形的内角和是外角和的倍,则这个多边形是六边形 D、若正多边形的一个外角等于 , 那么它是正十五边形5. 如图,窗户打开后,用窗钩AB可将其固定,其所运用的几何原理是( )
3. 具备下列条件的 , 不是直角三角形的是( )A、 B、 C、:::: D、4. 下列说法不正确的是( )A、多边形的内角和随多边形边数的增加而增加 B、多边形的外角和等于 C、若一个多边形的内角和是外角和的倍,则这个多边形是六边形 D、若正多边形的一个外角等于 , 那么它是正十五边形5. 如图,窗户打开后,用窗钩AB可将其固定,其所运用的几何原理是( ) A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间,线段最短6. 如图,在中,点 , 是边上的两点, , , 下列条件中不能判定≌的是( )
A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间,线段最短6. 如图,在中,点 , 是边上的两点, , , 下列条件中不能判定≌的是( )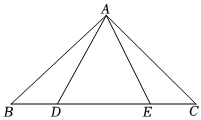 A、 B、 C、 D、7. 将正六边形与正五边形按如图所示方式摆放,公共顶点为 , 且正六边形的边与正五边形的边在同一条直线上,则的度数是( )
A、 B、 C、 D、7. 将正六边形与正五边形按如图所示方式摆放,公共顶点为 , 且正六边形的边与正五边形的边在同一条直线上,则的度数是( )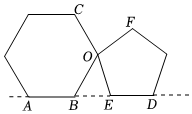 A、 B、 C、 D、8. 如图,小明从A点出发,沿直线前进16米后向左转45°,又向左转45°,…,照这样走下去,共走路程为( )
A、 B、 C、 D、8. 如图,小明从A点出发,沿直线前进16米后向左转45°,又向左转45°,…,照这样走下去,共走路程为( )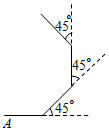 A、96米 B、128米 C、160米 D、192米9. 如图,在中,是高和的交点,且 , 已知 , , 则长为( )
A、96米 B、128米 C、160米 D、192米9. 如图,在中,是高和的交点,且 , 已知 , , 则长为( ) A、 B、 C、 D、10. 如图,是的中线,是的中线,是的中线,若 , 则等于( )
A、 B、 C、 D、10. 如图,是的中线,是的中线,是的中线,若 , 则等于( )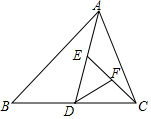 A、 B、 C、 D、11. 如图 , 已知线段 , , 求作 , 使 , , 张蕾的作法如图所示,则下列说法中一定正确的是( )
A、 B、 C、 D、11. 如图 , 已知线段 , , 求作 , 使 , , 张蕾的作法如图所示,则下列说法中一定正确的是( ) A、作的依据为 B、弧是以长为半径画的 C、弧是以点位圆心,为半径画的 D、弧是以长为半径画的12. 如图,在中, , , 为的中点,过点作交的延长线于点 , 且 , 下列说法正确的有个.( )
A、作的依据为 B、弧是以长为半径画的 C、弧是以点位圆心,为半径画的 D、弧是以长为半径画的12. 如图,在中, , , 为的中点,过点作交的延长线于点 , 且 , 下列说法正确的有个.( )
; ; ; ; .
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
13. 如果正n边形的一个内角与一个外角的比是3:2,则 .14. 如图,是的中线,已知的周长为 , 比长 , 则的周长为 .
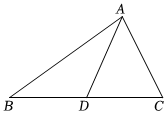 15. 如图所示, , 则
15. 如图所示, , 则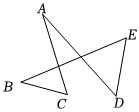 16. 如图,在中, , 将沿着直线折叠,点落在点的位置,则的度数是 .
16. 如图,在中, , 将沿着直线折叠,点落在点的位置,则的度数是 .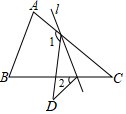 17. 已知在非直角三角形中, , 高与高所在直线交于点 , 则的度数是 .18. 如图,在中,设 , 与的平分线交于点 , 得;与的平分线相交于点 , 得;;与的平分线相交于点 , 得 , 则度数是 .
17. 已知在非直角三角形中, , 高与高所在直线交于点 , 则的度数是 .18. 如图,在中,设 , 与的平分线交于点 , 得;与的平分线相交于点 , 得;;与的平分线相交于点 , 得 , 则度数是 .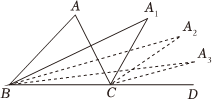
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
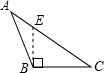
19. 一个等腰三角形的周长是28cm.(1)、已知腰长是底边长的3倍,求各边的长;(2)、已知其中一边长为6cm,求各边的长.20.(1)、已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.(2)、一个正多边形的内角和为1800°,求这个多边形的边数.21. 如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
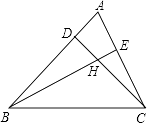 (1)、若BE⊥AC,CD⊥AB,求∠BHC的度数.(2)、若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.22. 如图,已知 , , , 求证: .
(1)、若BE⊥AC,CD⊥AB,求∠BHC的度数.(2)、若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.22. 如图,已知 , , , 求证: .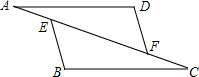 23. 如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
23. 如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.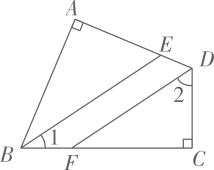 (1)、∠1与∠2有什么关系,为什么?(2)、BE与DF有什么关系?请说明理由.
(1)、∠1与∠2有什么关系,为什么?(2)、BE与DF有什么关系?请说明理由.