广西防城港市防城区2023-2024学年八年级上学期期中考试数学试题
试卷更新日期：2023-11-14 类型：期中考试
一、选择题(本大题共12小题，每小题3分，共36分．)
-
1. 下列四个图形分别是四届国际数学家大会的会标，其中是轴对称图形的是（ ）'A、
B、
C、
D、
2. 现有两根长度分别2cm和5cm的木棒．若要钉成一个三角形木架，则应选取的第三根木棒长为（ ）A、3cm B、4cm C、7cm D、9cm3. 如图，∠ACB>90°，AD⊥BC，BE⊥AC， CF⊥AB，垂足分别为点D、点E、点F，△ABC中BC边上的高是（ ）
A、CF B、CE C、BE D、AD4. 工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M、N重合，过角尺顶点C作射线OC，由此作法便可得△NOC≌△MOC，其依据是（ ）
A、ASA B、SAS C、SSS D、AAS5. 若一个正多边形的一个内角是120°，则这个正多边形的边数是（ ）A、6 B、5 C、4 D、36. 已知等腰三角形的一个角为80°，则该三角形的底角度数为． （ ）A、80° B、50°或80° C、50°或30° D、30°7. 如图，图中的两个三角形全等，则∠α= （ ）
A、49° B、50° C、59° D、71°8. 一块三角形的草坪，现要在草坪上建一个凉亭供大家休息，要使凉亭到草坪三边的距离相等，凉亭的位置应选在（ ）A、三角形三条边的垂直平分线的交点 B、三角形三条高所在直线的交点 C、三角形三条中线的交点 D、三角形三条角平分线的交点9. 若点M(-1，3)关于x轴对称点的坐标为P，则P的坐标为（ ）A、(-3，-1) B、(1，-3) C、(-3，1) D、(-1，-3)10. 如图，在△ABC中，线段AB的垂直平分线与AC相交于点D，连接BD，若AC=10，△BCD的周长为15，则BC的长为（ ）
A、5 B、8 C、10 D、1511. 如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的E处．若∠A=25° ，则∠BDC等于（ ）
A、50° B、60° C、70° D、75°12. 如图，在△OAB和△OCD中，OA=OB，OC=OD，OA>OC，∠AOB=∠COD=α，连接AC，BD交于点M，连接OM．下列结论：①AC=BD；②∠AMB=α；③∠OCA=∠ODB；④OM平分∠BOC．其中正确的是（ ）
A、①②③ B、②③④ C、①③④ D、①②③④二、填空题(本大题共6小题，每小题2分，共12分． )
-
13. 在日常生活中，我们通常采用如图的方法（斜钉上一块木条）来修理一张摇晃的椅子，请用数学知识说明这样做的依据是：.
14. 如图，在四边形ABCD中∠B=∠D =90°，请你添加一个适当的条件 ， 使得△ABC≌ △ADC．
15. 如图，已知AE是△ABC的中线，若△ABC的面积为7，则△ACE的面积为
16. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，并能绕O点自由旋转，若∠AOC=115° ，则∠BOD=
17. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A (0，1 )、B (3，1)、C (4，3)，如果以A、B、P为顶点的三角形与△ABC全等(点P与点C不重合)，满足条件的点P有个．
18. 如图，在△ABC中，AB=AC，D为BC的中点，AD=AE，若∠BAD=40°，则∠CDE=
三、解答题(本大题共8小题，共72分、解答应写出文字说明、证明过程或演算步骤．)
-
19. 如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAB=35°，∠B=50°，求∠C的度数．
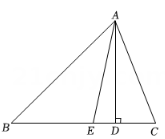20. 一个多边形，它的内角和比外角和的 倍多 求这个多边形的边数.21. 如图，在△ABC中，D是AB边上的一点，且AC=AD．
(1)、请用无刻度的直尺和圆规作出∠CAB的平分线AM，交BC于点M．(保留作图痕迹，不写作法，标明字母)(2)、连接DM，试猜想CM与DM的数量关系，并证明你的猜想22. 如图，在△ABC和△DEF中，BE=CF，AB=DE，AC=DF．
(1)、求证：△ABC≌△DEF．(2)、若BC=11，BF=16，求CE的长23. 如图，在△ABC中，AB=AC，CD⊥AB 于点D，BE⊥AC于点E，BE、CD相交于点O．
(1)、求证：△DBC≌△ECB；(2)、求证：DO=EO24. 如图，D为△ABC外角∠BCP平分线上一点，且DA=DB，DM⊥AP于点M，DN⊥BC于点N．
(1)、若BC=6，DM=2，求△BCD的面积；(2)、求证：BC=AM+CM．
