安徽省淮南市2023-2024学年八年级上学期数学月考考试试卷
试卷更新日期:2023-11-14 类型:月考试卷
一、选择题(每小题4分,10小题,共40分)
-
1. 如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是( )A、15 B、16 C、19 D、252. 要求画△ABC的边AB上的高,下列画法中,正确的是( )A、
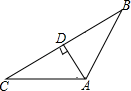 B、
B、 C、
C、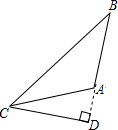 D、
D、 3. 若一个正n边形的每个外角为30°,则这个正n边形的边数是( )A、10 B、11 C、12 D、144. 如图的两个三角形全等,则的度数为( )
3. 若一个正n边形的每个外角为30°,则这个正n边形的边数是( )A、10 B、11 C、12 D、144. 如图的两个三角形全等,则的度数为( ) A、50° B、58° C、60° D、62°5. 如图,已知AM=CN , ∠MAB=∠NCD , 下列条件不能判定是ABMCDN的是( )
A、50° B、58° C、60° D、62°5. 如图,已知AM=CN , ∠MAB=∠NCD , 下列条件不能判定是ABMCDN的是( ) A、∠M=∠N B、BMDN C、AB=CD D、MB=ND6. 有公共顶点 , 的正五边形和正六边形按如图所示位置摆放,连接交正六边形于点 , 则的度数为( )
A、∠M=∠N B、BMDN C、AB=CD D、MB=ND6. 有公共顶点 , 的正五边形和正六边形按如图所示位置摆放,连接交正六边形于点 , 则的度数为( ) A、 B、 C、 D、7. 如图,在中,已知点D , E , F分别为 , , 的中点,且 , 则阴影部分面积( ) .
A、 B、 C、 D、7. 如图,在中,已知点D , E , F分别为 , , 的中点,且 , 则阴影部分面积( ) . A、1 B、2 C、3 D、48. 如图所示, , 的度数为( )
A、1 B、2 C、3 D、48. 如图所示, , 的度数为( ) A、 B、 C、 D、9. 如图,的面积为 , 平分 , 于P , 连接 , 则的面积为( )
A、 B、 C、 D、9. 如图,的面积为 , 平分 , 于P , 连接 , 则的面积为( ) A、 B、 C、 D、10. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A、 B、 C、 D、10. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )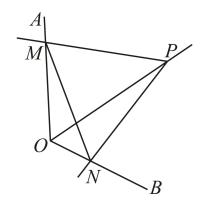 A、的值不变 B、 C、的长不变 D、四边形的面积不变
A、的值不变 B、 C、的长不变 D、四边形的面积不变二、填空题(每小题4分,6小题,共24分)
-
11. 如图,已知与交于点, , 要使 , 添加一个你认为合适的条件为 .
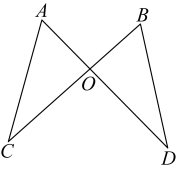 12. 如图,在ABC中, , , CD是的平分线,点E在AC上,且 , 则的度数为 .
12. 如图,在ABC中, , , CD是的平分线,点E在AC上,且 , 则的度数为 . 13. 如图,△ABC中,∠ABC与∠ACB的角平分线交于点O,若∠BAC=82°,则∠BOC=
13. 如图,△ABC中,∠ABC与∠ACB的角平分线交于点O,若∠BAC=82°,则∠BOC=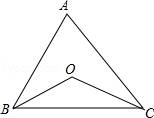 14. 在中,为边上的高,若 , 则 .15. 如图, , 点D在边上,延长交边于点F , 若 , 则 .
14. 在中,为边上的高,若 , 则 .15. 如图, , 点D在边上,延长交边于点F , 若 , 则 . 16. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
16. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
三、解答题
-
17. 如图,在中,点是边上的一点,连接 .
 (1)、若 , , 求的度数;(2)、若平分 , , , 试说明: .18. 如图,在中, , D是延长线上一点,E是的中点.
(1)、若 , , 求的度数;(2)、若平分 , , , 试说明: .18. 如图,在中, , D是延长线上一点,E是的中点. (1)、实践与操作:尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
(1)、实践与操作:尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).①作的平分线;
②连接并延长,交于点F .
(2)、猜想与证明:试猜想与有怎样的数量关系,并证明你的结论.19. 如图,在中,D是的中点,过点D的直线交于点F , 交的平行线于点G , 交于点E , 连接 . (1)、求证:;(2)、请你判断与的大小关系,并说明理由.20. 如图:在中,、分别是、两边上的高,在上截取 , 在射线上截取 , 连接、 . 猜想线段与的关系,并证明你的猜想.
(1)、求证:;(2)、请你判断与的大小关系,并说明理由.20. 如图:在中,、分别是、两边上的高,在上截取 , 在射线上截取 , 连接、 . 猜想线段与的关系,并证明你的猜想.

