2023年八年级上册数学人教版单元分层测试第十四章整式的乘法与因式分解 B卷

试卷更新日期：2023-11-13 类型：单元试卷

进入出卷网下载

一、选择题

1. 利用乘法公式计算正确的是（　　）

A、 ${(4 x - 3)}^{2} = 8 x^{2} + 12 x - 9$ B、 $(2 m + 5) (2 m - 5) = 4 m^{2} - 5$ C、 $(a + b) (a + b) = a^{2} + b^{2}$ D、 ${(4 x + 1)}^{2} = 16 x^{2} + 8 x + 1$

查看试题解析
2. 如果 $x^{2} + y^{2} = 8 ， x + y = 3$ ，则 $x y =$ （）

A、1 B、 $\frac{1}{2}$ C、2 D、 $- \frac{1}{2}$

查看试题解析
3. 如图，给出了正方形ABCD的面积的四个表达式，其中错误的是（）

A、 $(x - a) (x - a)$ B、 $x^{2} + a^{2} + 2 a x$ C、 $(x + a) (x + a)$ D、 $(x + a) a + x (x + a)$

查看试题解析
4. 设 $(x^{m - 1} y^{n + 2}) (x^{5 m} y^{2}) = x^{5} y^{7}$ ，则 ${(- \frac{1}{2} m)}^{n}$ 的值为（　　）

A、 $- \frac{1}{8}$ B、 $- \frac{1}{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
5. 若 $a + \frac{1}{a} = 3$ ，则 $\frac{a^{2}}{a^{4} + a^{2} + 1}$ 的值是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{1}{8}$ D、 $\frac{1}{9}$

查看试题解析
6. 已知 $a 、 b 、 c$ 是自然数，且满足 $2^{a} \times 3^{b} \times 4^{c} = 192$ ，则 $a + b + c$ 的取值不可能是（　　　）

A、5 B、6 C、7 D、8

查看试题解析
7. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1)$ 的计算结果的个位数字是（）

A、8 B、6 C、2 D、0

查看试题解析
8. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）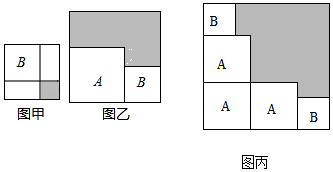

A、28 B、29 C、30 D、31

查看试题解析

二、填空题

9. 引入新数i，新数i满足分配律、结合律、交换律，已知 $i^{2} = - 1$ ，则 $(1 + i) (1 - i) =$ .

查看试题解析
10. 因式定理：对于多项式 $f (x)$ ，若 $f (a) = 0$ ，则 $(x - a)$ 是 $f (x)$ 的一个因式，并且可以通过添减单项式从 $f (x)$ 中分离出来.例如 $f (x) = 2 x^{3} - 3 x + 1$ ，由于 $f (1) = 0$ ，所以 $(x - 1)$ 是 $f (x)$ 的一个因式.于是 $f (x) = 2 x^{3} - 2 x^{2} + 2 x^{2} - 2 x - x + 1 = (x - 1) \times g (x)$ .则 $g (x) =$ .

查看试题解析
11. （x²﹣mx+6）（4x﹣2）的积中不含x的二次项，则m的值是．

查看试题解析
12. 将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为.

查看试题解析

三、计算题

13. 把下列各式分解因式.

(1)、 $a^{2} - 14 a b + 49 b^{2}$ ；

(2)、 $121 x^{2} - 144 y^{2} .$

查看试题解析

四、解答题

14. 若 $△ A B C$ 的三边长分别为a、b、c，且 $b^{2} + 2 a b = c^{2} + 2 a c$ ，判断 $△ A B C$ 的形状.

查看试题解析
15. 求证：对于任意自然数n，（n+7）²-（n-5）²都能被24整除.

查看试题解析
16. 问题再现：
数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
例如：利用图形的几何意义证明完全平方公式．
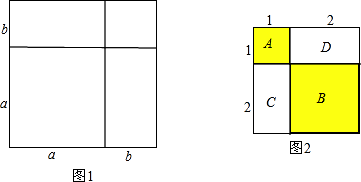
证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
这个图形的面积可以表示成：
（a+b）²或 a²+2ab+b²
∴（a+b）²=a²+2ab+b²
这就验证了两数和的完全平方公式．
类比解决：
①请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明：1³+2³=3²？
如图2，A表示1个1×1的正方形，即：1×1×1=1³
B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=2³
而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
由此可得：1³+2³=（1+2）²=3²
尝试解决：
②请你类比上述推导过程，利用图形的几何意义确定：1³+2³+3³= ▲ ．（要求写出结论并构造图形写出推证过程）．
问题拓广：
③请用上面的表示几何图形面积的方法探究：1³+2³+3³+…+n³= ▲ ．（直接写出结论即可，不必写出解题过程）

查看试题解析

五、综合题

17. 已知 $m + n = 3$ ， $m n = 2$ .

(1)、当 $a = 2$ 时，求 $a^{m} \cdot a^{n} - {(a^{m})}^{n}$ 的值；

(2)、求 ${(m - n)}^{2} + (m - 4) (n - 4)$ 的值.

查看试题解析
18. 例如：若a+b＝3，ab＝1，求a²+b²的值．
解：因为a+b＝3，所以（a+b）²＝9，即：a²+2ab+b²＝9，
又因为ab＝1，所以a²+b²＝7．
根据上面的解题思路与方法，解决下列问题：

(1)、若x+y＝8，x²+y²＝40，求xy的值；

(2)、填空：若（4﹣x）x＝5，则（4﹣x）²+x²＝；

(3)、如图所示，已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，CF＝2，长方形EMFD的面积是12，则x的值为．

查看试题解析
19. 有若干张正方形和长方形卡片如图①所示，其中A型、B型卡片分别是边长为a、b的正方形．C型卡片是长为a、宽为b的长方形．

(1)、【操作一】若用图①中的卡片拼成一个边长为a+3b的正方形，则需要A型卡片张，B型卡片张，C型卡片张；

(2)、【操作二】将C型卡片沿如图①所示虚线剪开后，拼成如图②所示的正方形，则选取C型卡片张，阴影部分图形的面积可表示为；

(3)、【操作三】如图③，将2张A型卡片和2张B型卡片无叠合的置于长为2a+b，宽为a+2b的长方形中．若图②中阴影部分的面积为4，图③中阴影部分面积为15，记每张A型、B型、C型卡片的面积分别为SA、SB、SC，求SA+SB+SC的值．

查看试题解析

2023年八年级上册数学人教版单元分层测试 第十四章 整式的乘法与因式分解 B卷

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023年八年级上册数学人教版单元分层测试第十四章整式的乘法与因式分解 B卷