2023-2024学年北师大版数学八年级上册7.4平行线的性质 同步练习（提升卷）
试卷更新日期：2023-11-12 类型：同步测试
一、选择题
-
1. 如图，△ABC≌△ADE ， 且AE∥BD ， ∠BAD=96°，则∠BAC的度数的值为（ ）
A、84° B、42° C、48° D、60°2.已知：如图，BD平分∠ABC，点E在BC上，AB∥EF，且∠FEC=100°，则∠ABD的度数为（ ）
A、60° B、50° C、40° D、30°3. 如图，将一张长方形纸条折叠，若边AB∥CD，则翻折角∠1与∠2一定满足的关系是（ ）
A、∠1＝2∠2 B、∠1+∠2＝90° C、∠1-∠2＝30° D、2∠1-3∠2＝30°4. 如图，点在上，≌ ， 当 ， 时，的度数为（ ）
A、 B、 C、 D、5. 如图是小明探索直线平行的条件时所用的学具，木条 ， ， 在同一平面内，经测量，要使木条 ， ， 要使木条与平行，则的度数应为（ ）
A、 B、 C、 D、6. 如图，直线 ， 点在上，点 ， 在上，平分交于点 ， ， 已知 ， 则的度数为（ ）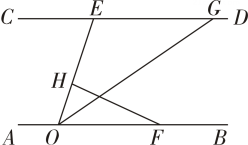
A、 B、 C、 D、7. 如图，直线 ， 点在直线上，点、在直线上，且 ， 平分 ， 若 ， 则的度数是（ ）
A、 B、 C、 D、8. 一个直尺和一个含45°的直角三角板按如图方式叠合在一起（三角板的两个顶点分别在直尺的边上），若∠1＝20°，则∠2的度数是（ ）
A、20° B、65° C、70° D、75°9. 已知，EF∥AB，CD⊥DF，∠2，∠3之间的关系满足（ ）
A、∠1+∠2+∠3＝180° B、∠2＝∠3+∠1 C、∠1+∠2-∠3＝90° D、∠2+∠3-∠1＝90°10. 一个含的直角三角尺和一把直尺按如图所示的位置摆放，若 ， 则的度数为（ ）
A、 B、 C、 D、二、填空题
-
11. 如图所示，将矩形纸片折叠，使点与点重合，点落在点处，折痕为 ， 若 ， 那么的度数为 ．
12. 如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1＝40°，则∠1，则∠2的度数为 ．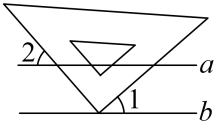
13. 将一副三角板中的两块直角三角尺的直角顶点 C 按如图方式叠放在一起，其中∠A＝60°，∠D＝30°，∠E＝∠B＝45°．当∠ACE＜90°，且点 E 在直线 AC 的上 方时，若这两块三角尺有两条边平行，则∠ACE＝ ．
14. 如图，把一张对面互相平行的纸条折成如图所示，是折痕，若 ， 则的度数为 ．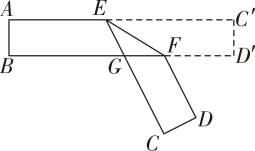
15. 如图，将一张长方形纸片沿折叠，点、分别落在点、的位置处，若 ， 则的度数是 ．
三、综合题
-
16. 如图，在四边形中，P为边上的一点，.、分别是、的角平分线.
(1)、若 ， 则的度数为 ， 的度数为；(2)、求证：；(3)、设 ， ， 过点P作一条直线，分别与 ， 所在直线交于点E、F，若 ， 直接写出的长（用含a的代数式表示）17. 如图，四边形中， ， ， 连接.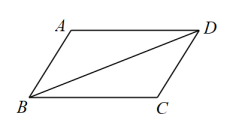
(1)、求证：；(2)、尺规作图（不写作法，保留作图痕迹）：作的垂直平分线 ， 分别交 ， 于点E，F；(3)、连接 ， 若 ， 求的度数.18. 问题情境在综合与实践课上，同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动如图1，已知两直线a，b且和直角三角形 ， ， ， .
(1)、在图1中， ， 求的度数；(2)、如图2，创新小组的同学把直线a向上平移，并把的位置改变，发现是一个定值，请写出这个定值，并说明理由；
(3)、缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，平分 ， 此时发现与又存在新的数量关系，请直接写出与的数量关系.
