2023-2024学年北师大版数学八年级上册7.3平行线的判定 同步练习(提升卷)
试卷更新日期:2023-11-12 类型:同步测试
一、选择题
-
1. 如图,能判定的是( )
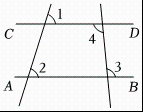 A、 B、 C、 D、2. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )
A、 B、 C、 D、2. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )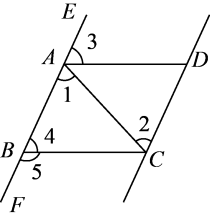 A、①②③ B、①②④ C、①③④ D、②③④3. 如图,下列推理不正确的是( )
A、①②③ B、①②④ C、①③④ D、②③④3. 如图,下列推理不正确的是( ) A、 , B、 , C、 , D、 ,4. 如图,由下列条件不能得到的是( )
A、 , B、 , C、 , D、 ,4. 如图,由下列条件不能得到的是( ) A、 B、 C、 D、5. 如图,直线 , 且直线 , 被直线 , 所截,则下列条件不能判定直线的是( )
A、 B、 C、 D、5. 如图,直线 , 且直线 , 被直线 , 所截,则下列条件不能判定直线的是( ) A、 B、 C、 D、6. 如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( )
A、 B、 C、 D、6. 如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( ) A、∠ADC=∠AEB B、 C、DE=GE D、CD=BE7. 如图, , 下列推理正确的是( )
A、∠ADC=∠AEB B、 C、DE=GE D、CD=BE7. 如图, , 下列推理正确的是( )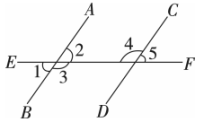
①若 , 则;②若 , 则;③若 , 则;④若 , 则.
A、①② B、②④ C、②③④ D、②③8. 如图,是的中线,E,F分别是和延长线上的点,且 , 连接 , , 下列说法:①和面积相等;②;③;④;⑤ . 其中正确的是( ) A、①② B、③⑤ C、①③④ D、①④⑤9. 如图,在中, , , , 则射线 与 ( )
A、①② B、③⑤ C、①③④ D、①④⑤9. 如图,在中, , , , 则射线 与 ( ) A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交10. 如图,下列条件中,不能判定的是( )
A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交10. 如图,下列条件中,不能判定的是( ) A、∠1=∠2 B、∠3=∠4 C、∠ADC+∠DCB=180° D、∠BAD+∠ADC=180°
A、∠1=∠2 B、∠3=∠4 C、∠ADC+∠DCB=180° D、∠BAD+∠ADC=180°二、填空题
-
11. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)
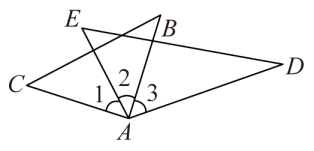 12. 如图, 给出下列命题∶ ① ;②;③ ;④ , 其中正确的命题有.
12. 如图, 给出下列命题∶ ① ;②;③ ;④ , 其中正确的命题有. 13. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.
13. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.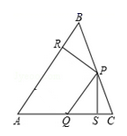 14. 如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确有:
14. 如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确有:①AD=EC;②BM=BN;③MN∥AC;④EM=MB.
 15. 如图, AD是 的中线,E,F分别是AD和AD延长线上的点,且 ,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有(填上正确的序号)
15. 如图, AD是 的中线,E,F分别是AD和AD延长线上的点,且 ,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有(填上正确的序号)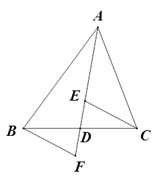
三、综合题
-
16. 如图,AE平分∠BAC,∠CAE=∠CEA.
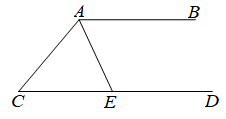 (1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.17. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 .
(1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.17. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 . (1)、求证:;(2)、若 , 连接平分平分 , 求的度数.18. 如图1,在五边形ABCDE中, , .
(1)、求证:;(2)、若 , 连接平分平分 , 求的度数.18. 如图1,在五边形ABCDE中, , . (1)、猜想AB与CD之间的位置关系,并说明理由;(2)、如图2,延长DE至F,连接BE,若 , , , 求∠C的度数.
(1)、猜想AB与CD之间的位置关系,并说明理由;(2)、如图2,延长DE至F,连接BE,若 , , , 求∠C的度数.

