2023-2024学年北师大版数学八年级上册7.1为什么要证明 同步练习(提升卷)
试卷更新日期:2023-11-12 类型:同步测试
一、单选题
-
1. 如图,在证明“内角和等于”时,延长至点 , 过点作 , 得到 , , 由于 , 可得到 , 这个证明方法体现的数学思想是( )
 A、数形结合 B、特殊到一般 C、一般到特殊 D、转化2. 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
A、数形结合 B、特殊到一般 C、一般到特殊 D、转化2. 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.已知:如图,直线 , 被直线所截, .
对说明理由.

方法:
如图,量角器测量所得 ,
对顶角相等 ,
角的度数相等 .
同位角相等,两直线平行 .
方法:
如图,已知 ,
对顶角相等 ,
等量代换 ,
同位角相等,两直线平行 .
下列说法正确的是( )
A、方法只要测量够组内错角进行验证,就能说明该定理的正确性 B、方法用特殊到一般的数学方法说明了该定理的正确性 C、方法用严谨的推理说明了该定理的正确性 D、方法还需说明其他位置的内错角,对该定理的说明才完整3. 如图,点是直线外一点,过点分别作 , , 则点、、三个点必在同一条直线上,其依据是( ) A、两点确定一条直线 B、同位角相等,两直线平行 C、过直线外一点有且只有一条直线与这条直线平行 D、平行于同一条直线的两条直线平行4. 如图,AC∥DF , AB∥DE , AC=DF , 下列条件中不能证明△ABC≌△DEF的是( )
A、两点确定一条直线 B、同位角相等,两直线平行 C、过直线外一点有且只有一条直线与这条直线平行 D、平行于同一条直线的两条直线平行4. 如图,AC∥DF , AB∥DE , AC=DF , 下列条件中不能证明△ABC≌△DEF的是( ) A、∠B=∠E B、EF=BC C、AB=DE D、EF∥BC5. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、
A、∠B=∠E B、EF=BC C、AB=DE D、EF∥BC5. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、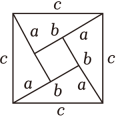 B、
B、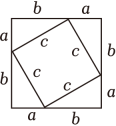 C、
C、 D、
D、 6. 数形结合是数学解题中常用的思想方法,可以使某些抽象的数学问题直观化、简洁化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材都安排了运用图形面积加以验证.下列图形中能验证的是( )A、
6. 数形结合是数学解题中常用的思想方法,可以使某些抽象的数学问题直观化、简洁化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材都安排了运用图形面积加以验证.下列图形中能验证的是( )A、 B、
B、 C、
C、 D、
D、 7. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )
7. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )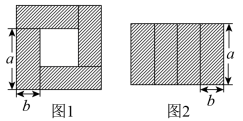 A、 B、 C、 D、8. 小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜 , 与墙面所成的角为 , 房顶与水平地面平行,小强在点M的正下方C处观察平面镜,恰能在M点看到水平地面上的点D.则的度数为( )
A、 B、 C、 D、8. 小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜 , 与墙面所成的角为 , 房顶与水平地面平行,小强在点M的正下方C处观察平面镜,恰能在M点看到水平地面上的点D.则的度数为( ) A、 B、 C、 D、9. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
A、 B、 C、 D、9. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.证法1:如图,
∵∠A=70°,∠B=63°,
且∠ACD=133°(量角器测量所得)
又∵133°=70°+63°(计算所得)
∴∠ACD=∠A+∠B(等量代换).
证法2:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质).
下列说法正确的是( )
 A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理10. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB
A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理10. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB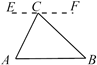 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 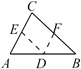 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 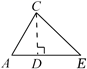 11. 定理:三角形的一个外角等于与它不相邻的两个内角的和.
11. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.
求证:∠ACD=∠A+∠B.
证法1:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质)
证法2:如图,
∵∠A=88°,∠B=58°,
且∠ACD=146°(量角器测量所得)
又∵146°=88°+58°(计算所得)
∴∠ACD=∠A+∠B(等量代换)
下列说法正确的是( )
 A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理
A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理二、填空题
-
12.
“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为S=a+ ﹣1,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是 , 并运用这个公式求得图2中多边形的面积是 .
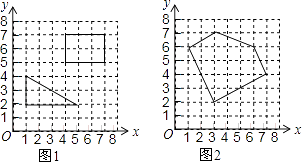
三、解答题
-
13. 阅读材料:我们已经学过幂的相关运算,其中幂的乘方是重要的性质之一,用式子表示为:(m、n为正整数),由此,幂的乘方运算反过来也是成立的,用式子表示为:(m、n为正整数),逆用幂的乘方的方法是:幂的底数不变,将幂的指数分解成两个因数的乘积,再转化成幂的乘方的形式.如 , 至于选择哪一个变形结果,要具体问题具体分析.例如,判断的末尾数字,我们可以采用如下的方法:
解析:的末尾数字等于的末尾数字
∵ , 又(n为正整数)的末尾数字均为6,
∴的末尾数字是的末尾数字,即为8.
∴的末尾数字为8
根据以上阅读材料,回答下列问题:
(1)、逆用幂的乘方,写出的末尾数字(2)、试判断的末尾数字14. 如图,已知 , 则 , , 之间的关系是: ▲ , 请写出你的证明过程. 15. 观察并验证下列等式:(1)、续写等式.(2)、根据上述等式中所体现的规律,猜想结论
15. 观察并验证下列等式:(1)、续写等式.(2)、根据上述等式中所体现的规律,猜想结论.
(3)、利用(2)中的结论计算:①
②
16. 如图,用硬纸板做成的四个全等的直角三角形,直角边的长分别为a和b,斜边长为c.可选取若干直角三角形纸板拼图,并根据拼图验证勾股定理. 请画出一种示意图并写出验证过程. 17. 发现:一个三位数的百位上数字为a,十位上数字为(a+1),个位上数字为(a+2);把这个三位数的百位上数字与个位上的数字交换得到一个新三位数,新三位数与原三位数的差是9的倍数.
17. 发现:一个三位数的百位上数字为a,十位上数字为(a+1),个位上数字为(a+2);把这个三位数的百位上数字与个位上的数字交换得到一个新三位数,新三位数与原三位数的差是9的倍数.验证:
(1)、①765—567=9× ;②通过列式计算,说明新三位数与原三位数的差是9的倍数;
(2)、延伸:新三位数与原三位数的和是正整数m的倍数,则m=____________,并说明理由.18. 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图所示,火柴盒的一个侧面ABCD倒下至AB'C'D'的位置,连接CC' ,设AB=a,BC=b,AC=c,请利用四边形BCC'D'的面积验证勾股定理:a2+b2=c2
-

