浙江省台州市路桥区2023-2024学年九年级第一学期10月阶段性检测数学试卷

试卷更新日期：2023-11-10 类型：月考试卷

进入 出卷网 下载

一、选择题：本大题有10个小题，每小题3分，共30分．

  • 1. 下列方程是一元二次方程的是（ ）
    A、x2－y＝1 B、x2＋2x－3＝0 C、x2＋1x＝3 D、x－5y＝6

    查看试题解析

  • 2. 若二次函数y＝ax2的图象经过点( l，－2 )，则它也经过（ ）
    A、(1，2) B、(－1，2) C、(－1，－2) D、(2，1)

    查看试题解析

  • 3. 用配方法解方程x2＋2x－3＝0，下列变形正确的是（ ）
    A、(x＋1)2＝－2 B、(x＋1)2＝2 C、(x－1)2＝4 D、(x＋1)2＝4

    查看试题解析

  • 4. 方程x2－2x－3＝0的一个实数根为m ， 则2023－m2＋2m的值是（ ）
    A、2020 B、2022 C、2023 D、2026

    查看试题解析

  • 5. 一个等腰三角形的两条边长分别是方程x2－7x＋10＝0的两根，则该等腰三角形的周长是（ ）
    A、9 B、12 C、13 D、12或9

    查看试题解析

  • 6. 二次函数y＝ax2＋bx＋c的部分对应值如列表，则方程ax2＋bx＋c＝0的一个解的范围是（ ）

    x

    6.17

    6.18

    6.19

    6.20

    y

    －0.03

    －0.01

    0.02

    0.04

    A、－0.01＜x＜0.02 B、6.17＜x＜6.18 C、6.18＜x＜6.19 D、6.19＜x＜6.20

    查看试题解析

  • 7. 二次函数y＝ax2＋bx＋c与一次函数y＝ax＋c在同一平面直角坐标系内的大致图象是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 8. 点P1(－1，y1)，P2(3，y2)，P3(5，y3)均在函数y＝－x2＋2x＋c的图象上，则（ ）
    A、y1＝y2＞y3 B、y1＞y2＞y3 C、y3＞y2＞y1 D、y3＞y1＝y2

    查看试题解析

  • 9. 如图是抛物线形拱桥的示意图，已知水面宽4m，顶点离水面2m．当水面宽6m时，水面下降（ ）
    A、1m B、1.5m C、2.5m D、4.5m

    查看试题解析

  • 10. 如图，二次函数y＝ax2＋bx＋c图象的对称轴为直线x＝1，有下列结论：①abc＜0；

    ②b－2a＜0；③a－b＋c＜0；④a＋b＞n(an＋b)(n≠1)．其中正确的是（ ）

    A、①②③ B、①②④ C、②③④ D、①③④

    查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分．

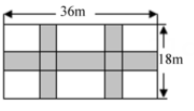
  • 11. 二次函数y＝2(x－1)2－3图象的顶点坐标为 ．

    查看试题解析

  • 12. 若1和－1是关于x的方程ax2＋bx＋c＝0的两个根，则a＋c＝ ．

    查看试题解析

  • 13. 如图，在平面直角坐标系中，二次函数y＝ax2＋bx＋c图象的对称轴为直线x＝2，与x轴的一个交点为(1，0)，则方程ax2＋bx＋c＝0的解为 ．

    查看试题解析

  • 14. 如图，在宽为18m ， 长为36m的矩形耕地上修建同样宽的三条道路(横向与纵向垂直)，把耕地分成若干小矩形块作为小麦试验田，假设试验田面积为450m2 ， 则道路宽为m ．

    查看试题解析

  • 15. 在平面直角坐标系中，将二次函数y＝x2＋2x－1的图象先沿x轴翻折，再向下平移3个单位，所得到的新的函数图象的解析式是 ．

    查看试题解析

  • 16. 如图，抛物线y＝－x2＋2x＋3与x轴交于A ， B两点(点A在点B的左侧)，与y轴交于点C ． 将抛物线沿y轴向下平移t(t＞0)个单位，当平移后的抛物线与线段OB有且只有一个交点时，则t的取值范围是 ．

    查看试题解析

三、解答题：本大题有8个小题，共66分．

  • 17. 解下列方程：
    (1)、2x2＋6x＋3＝0
    (2)、(x＋2)2＝3(x＋2)

    查看试题解析

  • 18. 已知二次函数图象的顶点坐标为(2，－1)，且过点(0，3)．
    (1)、求该二次函数解析式．
    (2)、判断点A(1，1)是否在该函数图象上．

    查看试题解析

  • 19. 已知关于x的一元二次方程(m－2)x2＋4x＋4－m2＝0，
    (1)、若m＝3，求方程的根.
    (2)、若方程有一个解是0，求m的值.

    查看试题解析

  • 20. 有长为30米的篱笆，一面利用墙(墙的最大可用长度为10米)，围成中间隔有一道篱笆(平行于AB)的矩形花圃，设花圃的一边AB为x米，面积为y平方米．
    (1)、求y关于x的函数表达式，并写出自变量x的取值范围．
    (2)、求矩形花圃的最大面积.

    查看试题解析

  • 21. 已知关于x的一元二次方程x2－(2m＋4)x＋m2＋4m＝0．
    (1)、求证：无论m取何值，此方程总有两个不相等的实数根．
    (2)、设方程的两个实数根分别为x1 ， x2 ， 若x12+x22=8 ， 求m的值.

    查看试题解析

  • 22. 已知二次函数y＝x2＋bx＋c经过A(1，1)和B(－1，－3)，二次函数与一次函数y＝－x－2交于C ， D两点．
    (1)、求二次函数的解析式．
    (2)、求三角形BCD的面积．
    (3)、结合图象直接写出不等式x2＋bx＋c＞－x－2的解集．

    查看试题解析

  • 23. 椒江某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“十一”国庆节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价5元，那么平均可多售出10件．
    (1)、设每件童装降价x元时，每天可销售 件，每件盈利 元；(用x的代数式表示)
    (2)、每件童装降价多少元时，平均每天盈利1200元．
    (3)、设专卖店每天销售这款童装可获利润W元，当x为多少时W最大，最大值是多少？

    查看试题解析

  • 24. 对于函数定义变换：当y≥0时，函数值不变；当y＜0时，函数值变为原来的相反数，我们把这种变换称为函数的“关联变换”，变换后的函数称为原函数的“关联函数”，“关联函数”与x轴的交点叫做“转折点”．

    如：一次函数y＝x－1，关联函数为y={x−1(x≥1)−x+1(x<1)} ， 这个关联函数的转折点是(1，0)．

    (1)、已知一次函数y＝2x－3，请直接写出它的“关联函数”的解析式和转折点．
    (2)、已知二次函数y＝x2－2x－3，点(a ， 4)在它的“关联函数”的图象上，求a的值．
    (3)、在平面直角坐标系内，有点M(－1，1)、N(3，1)，请直接写出a的取值范围是多少时，二次函数y＝x2－2x＋a的关联函数与线段MN恰有两个公共点．

    查看试题解析