山东省潍坊市2023-2024学年九年级上学期开学数学试卷（9月）

试卷更新日期：2023-11-10 类型：开学考试

进入出卷网下载

一、选择题（共6小题，共24分.）

1. 如图，把△ABC纸片的∠A沿DE折叠，点A落在四边形CBDE外，则∠1、∠2与∠A的关系是（　　）

A、∠1+∠2＝2∠A B、∠2-∠1＝2∠A C、∠2-∠A＝2∠1 D、2∠1+2∠A＝∠2

查看试题解析
2. 已知三个数 $a ， b ， c$ 满足 $\frac{a b}{a + b} = \frac{1}{5}$ ， $\frac{b c}{b + c} = \frac{1}{6}$ ， $\frac{c a}{c + a} = \frac{1}{7}$ ，则 $\frac{a b c}{a b + b c + c a}$ 的值是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{15}$ D、 $\frac{1}{20}$

查看试题解析
3. 将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°，在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P ， DF经过点C ，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M ， DF′交BC于点N ，则 $\frac{S_{△ P D M}}{S_{△ C D N}}$ 的值为（　　）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{3}$

查看试题解析
4. 定义一种关于整数n的“F”运算：
⑴当n是奇数时，结果为3n+5；
⑵当n是偶数时，结果是 $\frac{k}{2^{n}}$ （其中k是使 $\frac{k}{2^{n}}$ 是奇数的正整数），并且运算重复进行．
例如：取n＝58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n＝9，则第2023次运算结果是（　　）

A、6 B、7 C、8 D、9

查看试题解析
5. 如图，已知BO平分∠CBA ， CO平分∠ACB ，且MN∥BC ，设AB＝18，BC＝24，AC＝12，则MN的长是（　　）

A、13 B、 $\frac{25}{2}$ C、 $\frac{40}{3}$ D、14

查看试题解析
6. 如图①是3×3正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案，例如图②中的四幅图就视为同一种图案，则得到的不同图案共有（　　）

A、6种 B、5种 C、4种 D、3种

查看试题解析

二、多项选择题（本题共2小题，共8分；在每小题给出的选项中，有多项符合题目要求，全部选对得4分，有选错的得0分，部分选对的得2分）

7. 如图，点D为等边三角形ABC内的一点，DA＝5，DB＝4，DC＝3，将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′，下列结论正确的有（　　）

A、△ACD′可以由△ABD绕点A逆时针旋转60°得到 B、∠ADC＝150° C、点D到CD′的距离为4 D、 $S_{四边形 A B C D'} = 6 + \frac{25 \sqrt{3}}{4}$

查看试题解析
8. 甲乙两人骑自行车分别从A ， B两地同时出发相向而行，甲匀速骑行到B地，乙匀速骑行到A地，甲的速度大于乙的速度，两人分别到达目的地后停止骑行．两人之间的距离y（米）和骑行的时间x（秒）之间的函数关系图象如图所示，其中正确的结论有（　　）

A、a＝450 B、b＝150 C、甲的速度为8米/秒 D、当甲、乙相距50米时，甲出发了55秒或65秒

查看试题解析

三、填空题（本题共4小题，共20分，只要求填写最后结果，每小题填对得5分.）

9. 若关于x的不等式mx-n＞0的解集是x＜ $\frac{1}{7}$ ，则关于x的不等式（m+n）x＞n-m的解集是．

查看试题解析
10. 阅读材料：在求1+2+2²+2³+2⁴+…+2²⁰²²的值时，先设S＝1+2+2²+2³+2⁴+…+2²⁰²² ，将等式两边同时乘以2得：2S＝2+2²+2³+2⁴+2⁵+…+2²⁰²²+2²⁰²³ ，将下式减去上式得2S-S＝2²⁰²³-1，即S＝2²⁰²³-1，求得1+2+2²+2³+2⁴+…+2²⁰²²＝2²⁰²³-1，请你仿照此法计算：1+5+5²+5³+5⁴+…+5²⁰²³的值等于．

查看试题解析
11. 七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”．由边长为4 $\sqrt{2}$ 的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是．

查看试题解析
12. 如图是某校初中部美丽校园的一景，小明同学上学去班时要走过该段楼梯．已知本段楼梯共有10个阶梯，如果每步只允许走一个或两个阶梯，那么小明同学共有种方法走完本段楼梯．

查看试题解析

四、解答题（本题共4小题，共48分.解答应写出必要文字说明或演算步骤．）

13. 如图①，对角线互相垂直的四边形叫做垂美四边形．

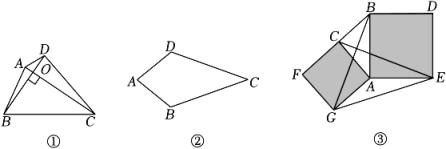(1)、【概念理解】如图②，在四边形ABCD中，AB＝AD ， CB＝CD ，问四边形ABCD是垂美四边形吗？请说明理由；

(2)、【性质探究】如图①，四边形ABCD的对角线AC ， BD交于点O ， AC⊥BD ．试证明：AD²+BC²＝AB²+CD²；

(3)、【解决问题】如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE ，连接CE ， BG ， GE ．已知AC＝8，AB＝10，求GE的长．

查看试题解析
14. 某学校计划今年国庆期间组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件完全一样的甲、乙两家宾馆可供选择，其收费标准均为每人每天120元，并且各自推出不同的优惠方案．
【问题信息】外出学习教师不超过100人．甲宾馆是35人以内（含35人）按标准收费，超过35人的，超出部分按九折收费；乙宾馆是45人以内（含45人）的按标准收费，超过45人的，超出部分按八折收费．
【问题设计】如果你是这个学校负责人，你会怎样选择宾馆？请你给出你的设计方案和理由．

查看试题解析
15. 数学来源于生活，生活中处处有数学，用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论．现有a克糖水，其中含有b克糖（a＞b＞0），则糖水的浓度（即糖的质量与糖水的质量比）为 $\frac{b}{a}$ ．

(1)、糖水实验一：加入m克水，则糖水的浓度为．生活经验告诉我们，糖水加水后会变淡，由此可以写出一个不等式，我们趣称为“糖水不等式”．

(2)、糖水实验二：
将“糖水实验一”中的“加入m克水”改为“加入m克糖”，则糖水的浓度为．根据生活经验，请你写出一个新的“糖水不等式” ．

(3)、请结合（2）探究得到的结论尝试证明：
设a、b、c为△ABC三边的长，求证： $\frac{c}{a + b} + \frac{a}{b + c} + \frac{b}{a + c} < 2$ .

查看试题解析
16. 综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．

(1)、操作判断
操作一：对折矩形纸片ABCD ，使AD与BC重合，得到折痕EF ，把纸片展平；
操作二：在AD上选一点P ，连接BP ，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM ， BM ．
如图1，当点M在EF上时，根据以上操作，写出一个度数为30°的角为；

(2)、迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q ，连接BQ ．
①如图2，当点M在EF上时，则∠MBQ＝ ▲ ；
②改变点P在AD上的位置（点P不与点A ， D重合）如图3，判断∠MBQ 与∠CBQ 的数量关系，并说明理由；

(3)、拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm ，当FQ＝1cm 时，请直接写出AP的长．

查看试题解析