北师版数学七年级上册周测卷(第四章 第1--4节) 培优卷
试卷更新日期:2023-11-10 类型:同步测试
一、选择题
-
1. 如图所示图形中,共有( )条线段.
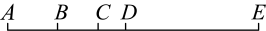 A、10 B、12 C、15 D、302. 手电筒发射出来的光线给我们的感觉是( )A、线段 B、射线 C、直线 D、折线3. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、44. 已知点在同一条直线上,且线段 , , 则两点间的距离是( )A、 B、 C、或 D、或5. 如图,延长线段到 , 使 . 若点恰为线段的中点,且 , 则( )
A、10 B、12 C、15 D、302. 手电筒发射出来的光线给我们的感觉是( )A、线段 B、射线 C、直线 D、折线3. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、44. 已知点在同一条直线上,且线段 , , 则两点间的距离是( )A、 B、 C、或 D、或5. 如图,延长线段到 , 使 . 若点恰为线段的中点,且 , 则( ) A、 B、 C、 D、6. 如图,点是线段的中点,是的中点,如果 , 那么( )
A、 B、 C、 D、6. 如图,点是线段的中点,是的中点,如果 , 那么( ) A、 B、 C、 D、7. 若 , , 则与的大小关系是( )A、 B、 C、 D、无法判断8. 如图,直线AB,CD相交于点O,∠2=3∠1,∠BOD=108°,则∠1=( )
A、 B、 C、 D、7. 若 , , 则与的大小关系是( )A、 B、 C、 D、无法判断8. 如图,直线AB,CD相交于点O,∠2=3∠1,∠BOD=108°,则∠1=( ) A、27° B、36° C、81° D、72°9. 一副三角尺按右上图所示位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果三角尺一边OB与90°刻度线重合,那么边OC与下列刻度线重合的是( )
A、27° B、36° C、81° D、72°9. 一副三角尺按右上图所示位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果三角尺一边OB与90°刻度线重合,那么边OC与下列刻度线重合的是( )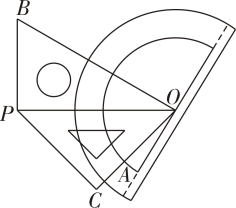 A、15°刻度线 B、30°刻 度线 C、45°刻度线 D、75°刻度线10. 一副三角板如图摆放,则的度数是( )
A、15°刻度线 B、30°刻 度线 C、45°刻度线 D、75°刻度线10. 一副三角板如图摆放,则的度数是( ) A、90° B、75° C、60° D、15°11. 将一副三角板按如图所示的不同方式摆放,则图中∠a与∠β一定相等的是( )A、
A、90° B、75° C、60° D、15°11. 将一副三角板按如图所示的不同方式摆放,则图中∠a与∠β一定相等的是( )A、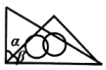 B、
B、 C、
C、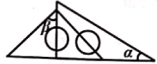 D、
D、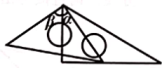 12. 如图,已知 , 若 , 则等于( )
12. 如图,已知 , 若 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 某高铁线路为往返于A市和E市,全长106千米,全线共设A、B、C、D、E五个车站,任意两站之间的距离都不相等,高铁集团要为乘客准备种车票,有种票价.14. 已知线段AB=7cm,在直线AB上画线段BC , 使它等于3cm,则线段AC=cm.15. 钟表上显示为3时40分,则时针与分针的夹角大小为度.16. 如图,在同一平面内,∠AOB=90°,∠AOC=25°,∠COD=50°,∠BOD>15°,则∠BOD的度数为
 17. 如图,将三个形状,大小完全一样的正方形的一个顶点重合放置, , , 则度.
17. 如图,将三个形状,大小完全一样的正方形的一个顶点重合放置, , , 则度.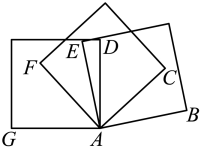 18. 如图,两块直角三角板的直角顶点O重合在一起,若 , 则∠BOC的度数为.
18. 如图,两块直角三角板的直角顶点O重合在一起,若 , 则∠BOC的度数为.
三、解答题
-
19. 已知线段AB=8cm,在直线AB上有一点C,且BC=4cm,M是线段AC的中点,画图并求线段AM的长.20. 已知线段AB=15cm,点C在线段AB上, ,D为BC的中点,求线段AD的长.21. 如图,已知OB,OC,OD是∠AOE内的三条射线,OB平分∠AOE,OD平分∠COE.
 (1)、若∠AOB=70°,∠DOE=20°,求∠BOC的度数.(2)、若∠AOE=136°,AO⊥CO,求∠BOD的度数.(3)、若∠DOE=20°,∠AOE+∠BOD=220°,求∠BOD的度数.22. 如图,已知线段 , 延长到 , 使得 , 反向延长到 , 使得 .
(1)、若∠AOB=70°,∠DOE=20°,求∠BOC的度数.(2)、若∠AOE=136°,AO⊥CO,求∠BOD的度数.(3)、若∠DOE=20°,∠AOE+∠BOD=220°,求∠BOD的度数.22. 如图,已知线段 , 延长到 , 使得 , 反向延长到 , 使得 . (1)、求线段的长;(2)、若为的中点,为线段上一点,且 , 求线段的长.23. 以直线上点为端点作射线 , 使 , 将直角的直角顶点放在点处.
(1)、求线段的长;(2)、若为的中点,为线段上一点,且 , 求线段的长.23. 以直线上点为端点作射线 , 使 , 将直角的直角顶点放在点处.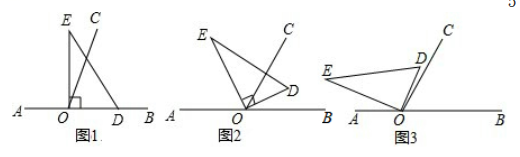 (1)、如图1,若直角的边放在射线上,则;(2)、如图2,将直角绕点按逆时针方向转动,使得平分 , 说明所在射线是的平分线;(3)、如图3,将直角绕点按逆时针方向转动,使得 . 求的度数.24. 材料阅读:如图①所示的图形,像我们常见的学习用品——圆规,我们不妨把这样图形叫做“规形图”.
(1)、如图1,若直角的边放在射线上,则;(2)、如图2,将直角绕点按逆时针方向转动,使得平分 , 说明所在射线是的平分线;(3)、如图3,将直角绕点按逆时针方向转动,使得 . 求的度数.24. 材料阅读:如图①所示的图形,像我们常见的学习用品——圆规,我们不妨把这样图形叫做“规形图”.
解决问题:
(1)、观察“规形图”,试探究与 , , 的关系(),并说明理由;(2)、请你直接利用以上结论,解决以下两个问题:①如图②,把一块三角尺放置在上,使三角尺的两条直角边 , 恰好经过点、 , 若 , 则 ▲ .
②如图③,平分 , 平分 , , , 求的度数.
25. 已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.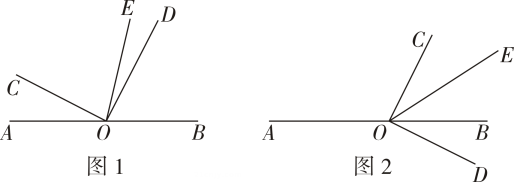 (1)、如图1,若∠AOC= 30°,求∠COE,∠BOD的度数.(2)、如图1,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).(3)、将图1中的∠COD绕顶点O顺时针旋转至图2的位置,探究∠AOC与∠DOE的度数之间的数量关系,并说明理由.
(1)、如图1,若∠AOC= 30°,求∠COE,∠BOD的度数.(2)、如图1,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).(3)、将图1中的∠COD绕顶点O顺时针旋转至图2的位置,探究∠AOC与∠DOE的度数之间的数量关系,并说明理由.