山东省菏泽市经开区多校联考2023-2024学年九年级上学期数学月考考试试卷(10月)
试卷更新日期:2023-11-09 类型:月考试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程中,属于一元二次方程的是( )A、 B、 C、 D、2. 在数学活动课上,老师让同学们判断一个由四根木条组成的四边形是否为矩形,下面是一个学习小组拟定的方案,其中正确的方案是( )A、测量四边形的三个角是否为直角 B、测量四边形的两组对边是否相等
C、测量四边形的对角线是否互相平分 D、测量四边形的其中一组邻边是否相等3. 根据下列表格的对应值,判断方程为常数的一个解的范围是( )A、 B、 C、 D、4. 如图,菱形 的对角线 、 相交于点 ,过点 作 于点 ,连接 ,若 , ,则菱形 的面积为( )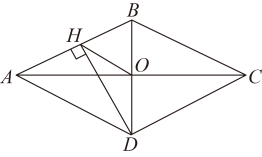 A、72 B、24 C、48 D、965. 如图,在任意四边形中, , , , 分别是 , , , 上的点,对于四边形的形状,以下结论中,错误的是( )
A、72 B、24 C、48 D、965. 如图,在任意四边形中, , , , 分别是 , , , 上的点,对于四边形的形状,以下结论中,错误的是( )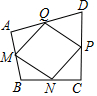 A、当 , , , 是各边中点,四边一定为平行四边形 B、当 , , , 是各边中点,且时,四边形为正方形 C、当 , 、 , 是各边中点,且时,四边形为菱形 D、当 , 、、是各边中点,且时,四边形为矩形6. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地号汽油价格六月底是元升,八月底是元升.设该地号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、7. 如图所示,在正方形中,是对角线上一点,过作 , , 垂足分别为、 , 连接 , 若 , 则的长为( )
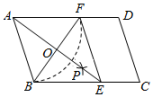
A、当 , , , 是各边中点,四边一定为平行四边形 B、当 , , , 是各边中点,且时,四边形为正方形 C、当 , 、 , 是各边中点,且时,四边形为菱形 D、当 , 、、是各边中点,且时,四边形为矩形6. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地号汽油价格六月底是元升,八月底是元升.设该地号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、7. 如图所示,在正方形中,是对角线上一点,过作 , , 垂足分别为、 , 连接 , 若 , 则的长为( )
 A、 B、 C、 D、8. 如图,在正方形外取一点 , 连接、、过点作的垂线交于点若 , 下列结论:
A、 B、 C、 D、8. 如图,在正方形外取一点 , 连接、、过点作的垂线交于点若 , 下列结论:
≌; ;
点到直线的距离为;
其中正确结论的序号是( )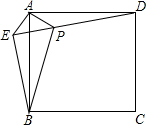 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
9. 若是关于的一元二次方程的解,则的值为 .10. 如图所示,在平行四边形中,以为圆心,长为半径画弧交于点 , 再分别以点、为圆心,大于为半径画弧,两弧交于一点 , 连接交于点 , 连接若 , , 则四边形的面积为 .
 11. 对于实数 , ,定义运算“ ”: ,例如: .根据此定义,则方程 的根为 .12. 如图,将矩形沿折叠,使顶点恰好落在边的中点上,若 , , 则的长为 .
11. 对于实数 , ,定义运算“ ”: ,例如: .根据此定义,则方程 的根为 .12. 如图,将矩形沿折叠,使顶点恰好落在边的中点上,若 , , 则的长为 . 13. 已知实数 , 满足 ,则代数式 的最小值等于.14. 如图,正方形边长为 , 点在边上,不与 , 重合 , 将沿直线折叠,点落在处,连接 , 将绕点顺时针旋转得到 , 连接 , , , 给出下列四个结论:
13. 已知实数 , 满足 ,则代数式 的最小值等于.14. 如图,正方形边长为 , 点在边上,不与 , 重合 , 将沿直线折叠,点落在处,连接 , 将绕点顺时针旋转得到 , 连接 , , , 给出下列四个结论:
≌; ;点是直线上动点,则的最小值为;
当时,的面积为 ,
其中正确的结论是 填写序号
三、解答题(本大题共9小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 解下列方程:(1)、用配方法解一元二次方程:;(2)、用因式分解法解方程;(3)、用公式法解方程;(4)、用合适的方法解方程 .16. 在菱形中, , , 求的长.
 17. 在矩形中, , , 求矩形的面积.
17. 在矩形中, , , 求矩形的面积.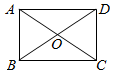 18. 如图,在平行四边形中,对角线与相交于点 , 于点 , 连接 , , .
18. 如图,在平行四边形中,对角线与相交于点 , 于点 , 连接 , , .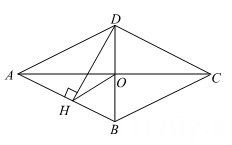 (1)、求证:四边形是菱形.(2)、求的周长19. 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
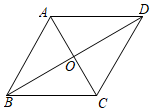
(1)、求证:四边形是菱形.(2)、求的周长19. 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.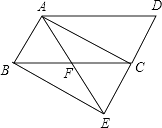 (1)、求证:AC=BE;(2)、若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.20. 已知关于的一元二次方程 .(1)、判断方程根的情况,并说明理由;(2)、若方程的一个根为 , 求的值和方程的另一个根.21. 阅读下面的材料,回答问题:
(1)、求证:AC=BE;(2)、若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.20. 已知关于的一元二次方程 .(1)、判断方程根的情况,并说明理由;(2)、若方程的一个根为 , 求的值和方程的另一个根.21. 阅读下面的材料,回答问题:解方程 ,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设 ,那么 ,于是原方程可变为 ①,解得
当 , 时,∴ ;
当 , 时,∴ ;
原方程有四个根: .
(1)、在由原方程得到方程①的过程中,利用法达到降次的目的,体现了数学的转化思想.(2)、试用上述方法解方程