四川省成都市新津县2023-2024学年重点中学九年级上学期第一次月考数学试卷
试卷更新日期:2023-11-09 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间2. 若单项式与 的和仍是单项式,则的值是( )A、 B、 C、 D、3. 已知关于x的分式方程 =1的解是负数,则m的取值范围是( )A、m≤3 B、m≤3且m≠2 C、m<3 D、m<3且m≠24. 关于的一元二次方程有两个实数根 , , 若 , 则的值( )A、或 B、或 C、 D、5. 已知二次函数 (其中 是自变量)的图象与 轴没有公共点,且当 时, 随 的增大而减小,则实数 的取值范围是( )A、 B、 C、 D、6. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形7. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为
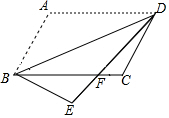 A、 B、 C、 D、8. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A、 B、 C、 D、8. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( ) A、 B、2 C、2 D、39. 如图,已知AB是 的直径,点P在BA的延长线上,PD与 相切于点D,过点B作PD的垂线交PD的延长线于点C,若 的半径为4, ,则PA的长为( )
A、 B、2 C、2 D、39. 如图,已知AB是 的直径,点P在BA的延长线上,PD与 相切于点D,过点B作PD的垂线交PD的延长线于点C,若 的半径为4, ,则PA的长为( )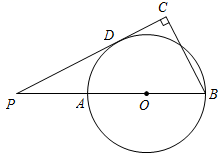 A、4 B、 C、3 D、2.510. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、
A、4 B、 C、3 D、2.510. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、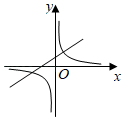 B、
B、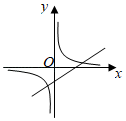 C、
C、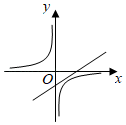 D、
D、
二、填空题(本大题共6小题,共18.0分)
-
11. 计算: .12. 因式分解: =.13. 若正多边形的每一个内角为135°,则这个正多边形的边数是 .
14. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点 处,当 为直角三角形时,BE的长为 15. 如图,为半圆内一点,为圆心,直径长为 , , , 将绕圆心逆时针旋转至 , 点在上,则边扫过区域图中阴影部分的面积为结果保留
15. 如图,为半圆内一点,为圆心,直径长为 , , , 将绕圆心逆时针旋转至 , 点在上,则边扫过区域图中阴影部分的面积为结果保留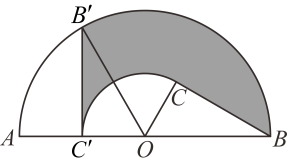 16. 如图,在正方形 的外侧,作等边 ,则 的度数是 .
16. 如图,在正方形 的外侧,作等边 ,则 的度数是 .
三、计算题(本大题共2小题,共12.0分)
-
17. 解分式方程: +1= .18. 正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
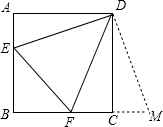 (1)、求证:EF=FM(2)、当AE=1时,求EF的长.
(1)、求证:EF=FM(2)、当AE=1时,求EF的长.四、解答题(本大题共4小题,共32.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 关于的一元二次方程有两个不等实根 , .(1)、求实数的取值范围.(2)、若方程两实根 , 满足 , 求的值.20. 如图,在中, , 过点的直线 , 为边上一点,过点作 , 交直线于 , 垂足为 , 连接、 .
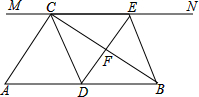 (1)、求证:;(2)、当在中点时,四边形是什么特殊四边形?说明你的理由;(3)、若为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.21. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
(1)、求证:;(2)、当在中点时,四边形是什么特殊四边形?说明你的理由;(3)、若为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.21. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.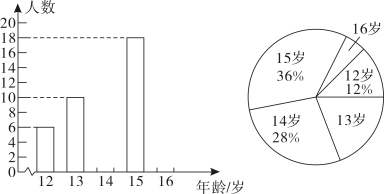
依据以上信息解答以下问题:
(1)、求样本容量;(2)、直接写出样本的平均数,众数和中位数;(3)、若该校一共有名学生,估计该校年龄在岁及以上的学生人数.22. “互联网”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条元,当售价为每条元时,每月可销售条.为了吸引更多顾客,该网店采取降价措施,据市场调查反映:销售单价每降元,则每月可多销售条.设每条裤子的售价为元为正整数 , 每月的销售量为条.(1)、直接写出与的函数关系式;(2)、设该网店每月获得的利润为元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出元资助贫困学生,为了保证捐款后每月利润不低于元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?