湖南省长沙市雅礼教育集团2023-2024学年九年级上学期能力测试数学试卷
试卷更新日期:2023-11-09 类型:月考试卷
一、填空题(本大题共16小题,共80.0分)
-
1. 下列因式分解正确的是 填序号
;
;
;
.2. 已知 , , , 则、、三个数的大小关系是 .3. 关于的一元二次方程有两个不相等的实数根,则的取值范围部是 .4. 一个数的小数部分用表示,为整数,且 , 记 , 的小数部分分别为 , , 则 .5. 关于的不等式组的整数解仅有个,则的取值范围是 .6. 一次函数与图象之间的距离等于 , 则的值为 .7. 函数的函数值随自变量的增大而减小,下列描述中:;函数图象与轴的交点为;函数图象经过第一象限;点在该函数图象上,正确的描述有 填写番号8. 我们知道,若则有或如图,直线与分别交轴于点、 , 则不等式的解集是 . 9. 若直线:与轴、轴分别交于点和点 , 直线:与轴、轴分别交于点和点 , 线段与的中点分别是 , , 点为轴上一动点.
9. 若直线:与轴、轴分别交于点和点 , 直线:与轴、轴分别交于点和点 , 线段与的中点分别是 , , 点为轴上一动点.
点的坐标为 ;
当的值最小时,点的坐标为 . 10. 方程和有一个公共根,则的值是 .11. 已知关于的方程的根都是整数,则满足条件的整数的值为 .12. 已知实数 , 满足 , , 且 , 则. 的值为 .13. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, , 点 , 分别在射线 , 上,长度始终保持不变 , 为的中点,点到 , 的距离分别为和 , 在此滑动过程中,猫与老鼠的距离的最小值为 .
10. 方程和有一个公共根,则的值是 .11. 已知关于的方程的根都是整数,则满足条件的整数的值为 .12. 已知实数 , 满足 , , 且 , 则. 的值为 .13. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, , 点 , 分别在射线 , 上,长度始终保持不变 , 为的中点,点到 , 的距离分别为和 , 在此滑动过程中,猫与老鼠的距离的最小值为 . 14. 如在正方形中,为上一点,过点作 , 交于 , 交对角线于 , 取的中点 , 连接 , , 下列结论:
14. 如在正方形中,为上一点,过点作 , 交于 , 交对角线于 , 取的中点 , 连接 , , 下列结论:
;
且;
;
≌;
若 , 则 ,
其中哪些结论是正确的 填序号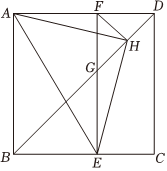 15. 已知 , , , , 均为非零实数,且满足 , 则的值为 .16. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:
15. 已知 , , , , 均为非零实数,且满足 , 则的值为 .16. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:
;
;
;
若方程有两个根和 , 且 , 则;
若方程有四个根,则这四个根的和为 .
其中正确的结论为 .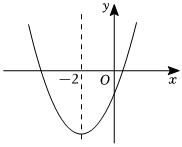
二、解答题(本大题共4小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知 , , 为正数,且 , 求的值.18. 已知:在中, , , 点为直线上一动点点不与、重合以为边作正方形 , 连接 .(1)、如图 , 当点在线段上时,求证:
;
.(2)、如图 , 当点在线段的反向延长线上时,且点、分别在直线的两侧,其它条件不变:
请直接写出、、三条线段之间的关系;
若连接正方形对角线、 , 交点为 , 连接 , 探究的形状,并说明理由. 19. 我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)、①在“平行四边形,矩形,菱形、正方形”中,一定是“十字形”的有 ;
19. 我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)、①在“平行四边形,矩形,菱形、正方形”中,一定是“十字形”的有 ;
若凸四边形是“十字形”, , , 则该四边形的面积为 ;
(2)、如图,以“十字形”的对角线与为坐标轴,建立如图所示的平面直角坐标系 , 若计“十字形”的面积为 , 记 , , , 的面积分别为: , , , , 且同时满足四个条件:;;“十字形”的周长为;;若为的中点,为线段上一动点,连接 , 动点从点出发,以的速度沿线段匀速运动到点 , 再以的速度沿线段匀速运动到点 , 到达点后停止运动,当点沿上述路线运动到点所需要的时间最短时,求点走完全程所需的时间及直线的解析式. 20. 如图,抛物线与轴分别交于点 , , 与轴交于点 .
20. 如图,抛物线与轴分别交于点 , , 与轴交于点 .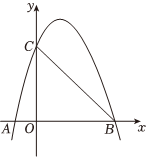 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、存在正实数 , , 当时,恰好满足 , 求 , 的值.