河北省保定市高碑店市2023-2024学年九年级上学期月考数学试题
试卷更新日期:2023-11-09 类型:月考试卷
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 如图,围绕在正方形四周的四条线段 , , , 中,长度最长的是( )
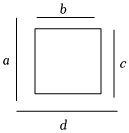 A、 B、 C、 D、2. 若方程是关于的一元二次方程,则“”可以是( )A、 B、 C、 D、3. 如图,为菱形的对角线,若 , 则的度数为( )
A、 B、 C、 D、2. 若方程是关于的一元二次方程,则“”可以是( )A、 B、 C、 D、3. 如图,为菱形的对角线,若 , 则的度数为( ) A、 B、 C、 D、4. 一元二次方程的解为( )A、 B、 C、 , D、 ,5. 菱形具有而平行四边形不一定具有的性质是( )A、对角线互相垂直 B、对边相等 C、对角相等 D、是中心对称图形6. 探索关于的一元二次方程的一个解的过程如下表所示:x
A、 B、 C、 D、4. 一元二次方程的解为( )A、 B、 C、 , D、 ,5. 菱形具有而平行四边形不一定具有的性质是( )A、对角线互相垂直 B、对边相等 C、对角相等 D、是中心对称图形6. 探索关于的一元二次方程的一个解的过程如下表所示:xx -3 -1 1
4
0.06
0.02
-0.03 -0.07 可以看出该方程的一个解应介于整数和之间,则整数 , 分别是( )
A、 , B、 , 1 C、1,4 D、4,57. 如图,在矩形中,对角线 , 相交于点 , 如果 , 那么的度数为( ) A、 B、 C、 D、8. 若关于的一元二次方程有一个解为1,则该方程的另一个解为( )A、0 B、2 C、3 D、9. 如图,若四边形是平行四边形,则下列结论中错误的是( )
A、 B、 C、 D、8. 若关于的一元二次方程有一个解为1,则该方程的另一个解为( )A、0 B、2 C、3 D、9. 如图,若四边形是平行四边形,则下列结论中错误的是( ) A、当时,它是矩形 B、当时,它是矩形 C、当时,它是矩形 D、当时,它是正方形10. 若一元二次方程有两个不相等的实数根,则“”所表示的数可以是( )A、 B、 C、 D、11. 在中, , 是的中点,求证: .
A、当时,它是矩形 B、当时,它是矩形 C、当时,它是矩形 D、当时,它是正方形10. 若一元二次方程有两个不相等的实数根,则“”所表示的数可以是( )A、 B、 C、 D、11. 在中, , 是的中点,求证: .证明:如图,延长至点 , 使 , 连接 , .
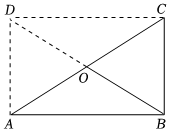
……
,
.
下面是“……”部分被打乱顺序的证明过程:①∴四边形是平行四边形;②∵;③∵ , ;④∴四边形是矩形.
A、③①②④ B、③②①④ C、②③①④ D、②①③④12. 某节数学课上,老师让学生解关于的方程 , 下面是这三位同学的解答过程:小逸
小明
小琛
两边同时除以 , 得 .
整理得 ,
配方得 ,
, ,
, .
移项得 ,
,
或 ,
, .
下列选项中,说法正确的是( )
A、只有小明的解法正确 B、只有小琛的解法正确 C、只有小逸的解法错误 D、小逸和小琛的解法都是错误的13. 如图,在平面直角坐标系中,四边形是正方形,已知点的坐标为 , 则点的坐标为( )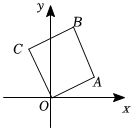 A、 B、 C、 D、14. 已知关于的一元二次方程有一个非零实数根 , 则的值为( )A、1 B、 C、0 D、215. 如图,矩形绿地的长为 , 宽为 , 将此绿地的长、宽各增加相同的长度后,绿地面积增加了 , 设绿地的长、宽增加的长度为 , 则下面所列方程正确的是( )
A、 B、 C、 D、14. 已知关于的一元二次方程有一个非零实数根 , 则的值为( )A、1 B、 C、0 D、215. 如图,矩形绿地的长为 , 宽为 , 将此绿地的长、宽各增加相同的长度后,绿地面积增加了 , 设绿地的长、宽增加的长度为 , 则下面所列方程正确的是( ) A、 B、 C、 D、16. 如图,把一张矩形纸片按如下方法进行两次折叠:第一次将边折叠到边上得到 , 抓痕为 , 连接 , , 第二次将沿着折叠,边恰好落在边上.若 , 则的长为( )
A、 B、 C、 D、16. 如图,把一张矩形纸片按如下方法进行两次折叠:第一次将边折叠到边上得到 , 抓痕为 , 连接 , , 第二次将沿着折叠,边恰好落在边上.若 , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
-
17. 把一元二次方程化成的一般形式,其中 , 则常数项 .18. 若关于的一元二次方程的两个根分别是与 , 则的值为 , 方程的根为 .19. 如图,菱形的对角线 , 相交于点 , 过点作于点 , 连接 .
 (1)、 . (填“”、“”或“=”)(2)、若 , 菱形的面积为4,则的长为 .
(1)、 . (填“”、“”或“=”)(2)、若 , 菱形的面积为4,则的长为 .三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 嘉淇同学解方程的过程如下表表示.
解方程: .
解: , ……第一步
, ……第二步
, . ……第三步
(1)、嘉淇同学是用(“配方法”、“公式法”或“因式分解法”)求求解的,从第步开始出现错误.(2)、请你用不同于(1)中的方法解该方程.21. 如图,矩形的对角线 , 相交于点 , 过点作的平行线交的延长线于点 . (1)、求证: .(2)、若 , , 求的长.22. 定义:如果关于的一元二次方程满足 , 那么我们称这个方程为“完美方程”.(1)、下面方程是“完美方程”的是 . (填序号)
(1)、求证: .(2)、若 , , 求的长.22. 定义:如果关于的一元二次方程满足 , 那么我们称这个方程为“完美方程”.(1)、下面方程是“完美方程”的是 . (填序号)① ② ③
(2)、已知是关于的“完美方程”,若是此“完美方程”的一个根,求的值.23. 如图,在中, , 分别是边 , 上的点,连接 , , 与交于点 , . 添加下列条件之一使成为菱形:①;② , . (1)、你添加的条件是 ▲ (填序号),并证明.(2)、在(1)的条件下,若 , 的周长为4,求菱形的边长.24. 如图1,在中,点 , 在对角线上, , , 过点作交的延长线于点 .
(1)、你添加的条件是 ▲ (填序号),并证明.(2)、在(1)的条件下,若 , 的周长为4,求菱形的边长.24. 如图1,在中,点 , 在对角线上, , , 过点作交的延长线于点 .
图1
(1)、求证:四边形是矩形.(2)、如图2,连接 , 当时,判断四边形的形状,并说明理由. 图225. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶,在“创建文明城市”期间,计划将头盔降价销售,经调查发现,每降价1元,每月多售出20顶,已知头盔的进价为每顶50元.(1)、若每顶头盔降价10元,则每月可销售顶头盔,每月销售利润为元.(2)、若商店为了减少库存,准备降价销售这批头盔,同时确保每月的销售利润为7500元,求头盔的销售单价.(3)、若降价销售这批头盔,每月的利润能否达到9000元?请说明理由.26. 在正方形中,为对角线上一点,连接 , .
图225. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶,在“创建文明城市”期间,计划将头盔降价销售,经调查发现,每降价1元,每月多售出20顶,已知头盔的进价为每顶50元.(1)、若每顶头盔降价10元,则每月可销售顶头盔,每月销售利润为元.(2)、若商店为了减少库存,准备降价销售这批头盔,同时确保每月的销售利润为7500元,求头盔的销售单价.(3)、若降价销售这批头盔,每月的利润能否达到9000元?请说明理由.26. 在正方形中,为对角线上一点,连接 , . (1)、如图1,图中的全等三角形有(不必证明).(2)、如图2,为延长线上一点,且 , 交于点 . 判断的形状,并说明理由.(3)、如图3,过点作交的延长线于点 .
(1)、如图1,图中的全等三角形有(不必证明).(2)、如图2,为延长线上一点,且 , 交于点 . 判断的形状,并说明理由.(3)、如图3,过点作交的延长线于点 .①求证: .
②若 , , 请直接写出的长.