广东省深圳市龙岗区2023-2024学年七年级（上）期中数学试卷

试卷更新日期：2023-11-09 类型：期中考试

进入出卷网下载

一、选择题(本题共10小题，每题3分，共30分)

1. 中国是最早采用正负数表示相反意义的量的国家，如果将”收入60元”记作”+60元”，那么“支出40元”记作（）

A、+40元 B、-40元 C、+20元 D、20元

查看试题解析
2. 2023年2月10号，神舟十五号航天员乘组圆满完成了他们的首次出舱任务，飞船的速度约为每小时28000千米（）

A、2.8×10⁴ B、2.8×10⁵ C、2.8×10⁶ D、28×10³

查看试题解析
3. 如图所示的平面图形绕直线I旋转一周，可以得到的立体图形是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、(-1)+(-3) =4 B、(-1)-(-3)=-2 C、(-1)×(-3)=3 D、(-1)÷(-3)=-3

查看试题解析
5. 用一个平面去截一个正方体，则截面的形状不可能为（）

A、等腰三角形 B、梯形 C、正七边形 D、五边形

查看试题解析
6. 一个矩形的周长为30，若矩形的一边长用字母x表示，则此矩形的另一边长可表示为（）

A、15-x B、30-x C、30-2x D、15+x

查看试题解析
7. 下列说法正确的是（）

A、绝对值相等的两数相等 B、若a、b互为相反数，则 $\frac{a}{b}$ =-1 C、若a²=b² ，则|a|=|b| D、-a上定是一个负数

查看试题解析
8. 若(a-1)²+|b-2|=0，则a+b的值为（）

A、1 B、-1 C、3 D、-3

查看试题解析
9. ”磁力健构片”通过磁铁连接重心，可以轻松制作成球体、锥体、正方体等百种造型，立体提拉魔幻成型，直观立体，是全面开发脑力的益智玩具．如图所示的平面图形经过立体提拉后，会成型为（）

A、圆锥 B、长方体 C、五棱柱 D、圆柱

查看试题解析
10. 将一些完全相同的棋子按如图所示的规律摆放，第①个图中有4颗棋子，第②个图中有7颗棋子，第③个图中有12颗棋子，……，按此规律，则第⑨个图中棋子的颗数是（）

A、52 B、67 C、84 D、101

查看试题解析

二、填空题(本题共5小题，每小题3分，共15分)

11. 某地一天早晨的气温是3℃，中午气温下降了9℃，则晚上的气温为 ℃．

查看试题解析
12. 在数轴上点A、B表示的数分别是-3和5，则线段AB长是。

查看试题解析
13. 如图是正方体的一种展开图，表面上的语句为北京2022年冬奥会和冬残奥会的主题口号”一起向未来！”，那么在正方体的表面与”！”相对的汉字是。

查看试题解析
14. 对于任意有理数a、b，定义一种新运算” ⊕”，规则如下： a⊕b=ab+(a-b)， (3-2)=7，则(-5)⊕4= ．

查看试题解析
15. 如图，在数轴上点A、B表示的数分别为-2、4，若点M从A点出发以每秒5个单位长度的速度沿数轴向右匀速运动，点N从B出发以每秒4个单位长度的速度沿数轴匀速运动，设点M、N同时出发，运动时间为t秒，经过秒后，M、N两点间的距离为12个单位长度．

查看试题解析

三、解答题（本题共7题，共55分）

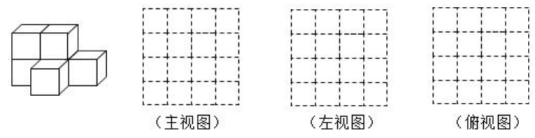
16. 计算：

(1)、18+(-12)+(-18)

(2)、 $1 \frac{3}{7} + (- 2 \frac{1}{3}) + 2 \frac{4}{7} + (- 1 \frac{2}{3})$

(3)、 $(- \frac{1}{12} - \frac{1}{36} + \frac{1}{6}) \times (- 36)$

(4)、-1²⁰²³-(-2)³-(-2)×(-3)

查看试题解析
17. 如图是由棱长都为1cm的6块小正方体组成的简单几何体．请在方格中分别画出从正面、左面和上面观察该几何体时看到的形状图．

查看试题解析
18. 若a，b互为相反数，c，d互为倒数，|m|=4，则：

(1)、a+b= ． cd= ． m= ．

(2)、求 $\frac{a + b}{3}$ +m²-5cd的值．

查看试题解析
19. 有理数a、b、c在数轴上的位置如图：

(1)、判断正负，用”>“或”<“填空：
b-c0；a+b0；c-a0．

(2)、化简：|b|+|a|+|c-a|．

查看试题解析
20. 有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，称后的记录如下：
回答下列问题：

(1)、这8筐白菜中最接近标准重量的这筐白菜重千克

(2)、这8筐白菜中最重的重千克：最轻的重千克．

(3)、若白菜每千克售价2元，则出售这8筐白菜可卖多少元？

查看试题解析
21. 如图是一张长方形纸片，长方形的长为10cm，宽为6cm．若将此长方形纸片绕它的一边所在直线旋转一周，得到一个几何体．

(1)、这个几何体的名称是，这个现象用数学知识解释为 (选填“点动成线”“线动成面”或”面动成体”)；

(2)、求得到的这个几何体的体积．(结果保留π)

查看试题解析
22. 在数轴上，把原点记作点O，表示数1的点记作点A．对于数轴上任意一点P (不与点O，点A重合)，记作 $\hat{P}$ ，即 $\hat{P}$ = $\frac{P O}{P A}$ ，例如：当点P是线段OA的中点时，所以 $\hat{P}$ =1．

(1)、如图，点P₁ ， P₂ ， P₃为数轴上三个点，点P₁表示的数是 $- \frac{1}{4}$ ，点P₂与P₁关于原点对称．
① $\hat{P}$ ₂=
②比较 $\hat{P_{1}}$ ， $\hat{P_{2}}$ ， $\hat{P_{3}}$ 的大小（用“<”连接）

(2)、数轴上的点M满足OM= $\frac{1}{3}$ OA，求 $\hat{M}$ ：

(3)、数轴上的点P表示有理数p，已知 $\hat{P}$ <100且 $\hat{P}$ ，则所有满足条件的p的倒数之和为

查看试题解析