浙江省宁波市江北区惠贞书院2022-2023学年九年级(上)期中数学试卷
试卷更新日期:2023-11-09 类型:期中考试
一、选择题(本题有10小题,每小题4分,共40分。请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
-
1. 某病毒的直径约为0.00000013m,则数据0.00000013m用科学记数法表示为( )A、0.13×10-6 B、1.3×10-7 C、0.13×10-7 D、1.3×10-82. 如图是由5个相同大小的正方体搭成的几何体,则它的主视图是( )
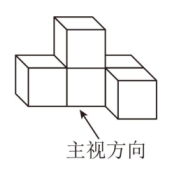 A、
A、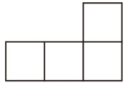 B、
B、 C、
C、 D、
D、 3. 假设命题“a>0"不成立,那么a与0的大小关系只能是( )A、a≠0 B、a≤0 C、a=0 D、a<04. 若点A (-5,y1),B (1,y2),C(5,y3)都在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y1<y3<y2 D、y3<y1<y25. 已知⊙O的半径为2,点P到圆心O的距离为 ,则点P在( )A、圆内 B、圆上 C、圆外 D、不能确定6. 某射击运动员在训练中射击了10次,成绩如图所示:
3. 假设命题“a>0"不成立,那么a与0的大小关系只能是( )A、a≠0 B、a≤0 C、a=0 D、a<04. 若点A (-5,y1),B (1,y2),C(5,y3)都在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y1<y3<y2 D、y3<y1<y25. 已知⊙O的半径为2,点P到圆心O的距离为 ,则点P在( )A、圆内 B、圆上 C、圆外 D、不能确定6. 某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是1.27. 如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )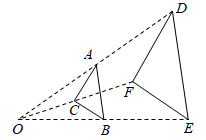 A、1:2 B、1:4 C、1:3 D、1:98. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC,若AB=BC=1,∠AOB=α,则tan∠BOC的值为( )
A、1:2 B、1:4 C、1:3 D、1:98. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC,若AB=BC=1,∠AOB=α,则tan∠BOC的值为( ) A、sinα B、cosα C、tanα D、9. 定义符号min{a,b}的含义为:当a≥b时, min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,-3}=-3,min{-4,-2}=-4.已知一种关于x的新函数y=min{x+1,-x+m},且m>-1,则关于y的函数下面说法错误的是( ).A、若m=1,则当y≤-2时,则x≤-3或x≥3 B、当函数图象经过(0,)时,该函数图象的最高点的坐标为( , ) C、( , y1) ( , y2)是函数图象上的两点,则y1>y2 D、当1≤x≤2时,函数y的最大值为3,则m=3或510. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )
A、sinα B、cosα C、tanα D、9. 定义符号min{a,b}的含义为:当a≥b时, min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,-3}=-3,min{-4,-2}=-4.已知一种关于x的新函数y=min{x+1,-x+m},且m>-1,则关于y的函数下面说法错误的是( ).A、若m=1,则当y≤-2时,则x≤-3或x≥3 B、当函数图象经过(0,)时,该函数图象的最高点的坐标为( , ) C、( , y1) ( , y2)是函数图象上的两点,则y1>y2 D、当1≤x≤2时,函数y的最大值为3,则m=3或510. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )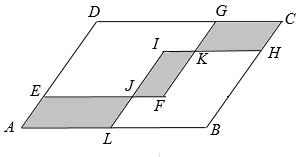 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式: -9= .12. 如图所示的网格是正方形网格,则点 , , 是网格线交点 .
 13. 某校开展读书日活动,小亮和小莹分别从校图书馆的“科技”、“文学”、“艺术”三类书籍中随机地抽取一本,抽到同一类书籍的概率是 .14. 如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为
13. 某校开展读书日活动,小亮和小莹分别从校图书馆的“科技”、“文学”、“艺术”三类书籍中随机地抽取一本,抽到同一类书籍的概率是 .14. 如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为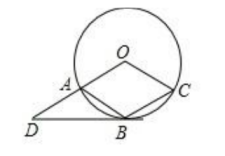 15. “地摊经济”一时兴起,小惠计划在夜市销售一款产品,进价每件40元,售价每件110元,每天可以销售20件,每销售一件需缴纳摊位管理费用a元(a>0).未来30天,这款产品将开展“每天降价1元”的大促销活动,即从第一 天起每天的单价均比前天降1元,通过市场调研发现:该产品单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳摊位管理费用后的利润随天数t ( t为正整数)的增大而增大,则a的取值范围应为.16. 如图,已知矩形ABCD,AB= , BC=3,点P是在直线AB的右侧的一动点,且∠APB=60°,CE=-3.点P到直线AB距离的最大值是;PE的最小值是
15. “地摊经济”一时兴起,小惠计划在夜市销售一款产品,进价每件40元,售价每件110元,每天可以销售20件,每销售一件需缴纳摊位管理费用a元(a>0).未来30天,这款产品将开展“每天降价1元”的大促销活动,即从第一 天起每天的单价均比前天降1元,通过市场调研发现:该产品单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳摊位管理费用后的利润随天数t ( t为正整数)的增大而增大,则a的取值范围应为.16. 如图,已知矩形ABCD,AB= , BC=3,点P是在直线AB的右侧的一动点,且∠APB=60°,CE=-3.点P到直线AB距离的最大值是;PE的最小值是
三、解答题(本题有8小题,第17、18、19题每题8分,第20、21题10分,第22、23、24题每题12分,共80分)
-
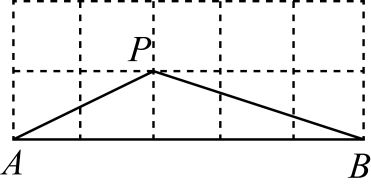
17. 按要求计算:(1)、计算:(2)、先化简,再求值: , 其中y=-2.18. 在6×6的方格纸中,点A,B,C都在格点上,仅用无刻度尺画图(保留画图痕迹,不写画法).

⑴在图1中,画△ABC的中线CD.
⑵在图2中,在AB边上找一点P,使点P到AC、BC的距离之比为2:3.
19. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查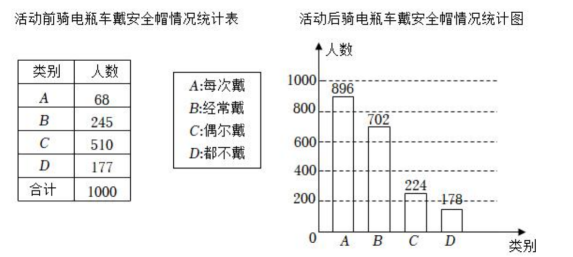 (1)、宣传活动前,在抽取的市民中哪一类别的 人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178, 比活动前增加了1人,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.20. 如图1是一台刷脸支付仪,由底柱、水平托板、支撑板和电子器材构成,图2是其上半部分的侧面示意图.电子器材长AC=16cm,水平托板DE离地面的高度为120cm,∠CBD=75°,已知摄像头在点A处,支撑点B是AC的中点,支撑板BD可绕点D转动.
(1)、宣传活动前,在抽取的市民中哪一类别的 人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178, 比活动前增加了1人,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.20. 如图1是一台刷脸支付仪,由底柱、水平托板、支撑板和电子器材构成,图2是其上半部分的侧面示意图.电子器材长AC=16cm,水平托板DE离地面的高度为120cm,∠CBD=75°,已知摄像头在点A处,支撑点B是AC的中点,支撑板BD可绕点D转动. (1)、如图2,求摄像头(点A)离地面的高度h (精确到0.1cm);(2)、如图3,为方便使用,把AC绕点B逆时针旋转15° 后,使点C落在水平托板DE上,求α(精确到0.1° ).(参考数据: tan26.6° ≈0.5;≈1.41,≈1.73)21. 如图所示,抛物线y=ax2+c与x轴交于A,B两点,顶点为C,且位于x轴的下方,若点P (1,-3),B(4,0).
(1)、如图2,求摄像头(点A)离地面的高度h (精确到0.1cm);(2)、如图3,为方便使用,把AC绕点B逆时针旋转15° 后,使点C落在水平托板DE上,求α(精确到0.1° ).(参考数据: tan26.6° ≈0.5;≈1.41,≈1.73)21. 如图所示,抛物线y=ax2+c与x轴交于A,B两点,顶点为C,且位于x轴的下方,若点P (1,-3),B(4,0). (1)、求该抛物线的函数表达式.(2)、若D是抛物线上一点,且满足∠DPO=∠POB,求点D的坐标.22. 根据下列题目要求,解答下列问题:
(1)、求该抛物线的函数表达式.(2)、若D是抛物线上一点,且满足∠DPO=∠POB,求点D的坐标.22. 根据下列题目要求,解答下列问题: (1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.23. 对于给定的两个函数,任取自变量x的一个值,当x<0时;它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为“伴随”函数,例如:一次函数y=x-3,它的“伴随”函数为y=.(1)、已知点M (-2,1)在一次函数y=-mx+1的“伴随”函数的图象上,求m的值.(2)、已知二次函数y=-x2+4x-
(1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.23. 对于给定的两个函数,任取自变量x的一个值,当x<0时;它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为“伴随”函数,例如:一次函数y=x-3,它的“伴随”函数为y=.(1)、已知点M (-2,1)在一次函数y=-mx+1的“伴随”函数的图象上,求m的值.(2)、已知二次函数y=-x2+4x-①当点A (a,)在这个函数的“伴随”函数的图象上时,求a的值.
②当-3≤x≤3时,函数y=-x2+4x-的“伴随”函数是否存在最大值或最小值,若存在,请求出最大值或最小值;若不存在,请说明理由.
24. 已知△ABC内接于⊙O,AB=BC,AD⊥BC于点D. (1)、如图1,求证:∠ABC=2∠CAD;(2)、如图2,延长AD,交⊙O于点E,点F在线段AD上,DF=DE,过点F作FG⊥AC,垂足为点G,求证: AG=CG;(3)、如图3,在(2)的条件下,连接CE,点H在线段BD上,CH=CE,连接AH、OH,若AB=10, S△ABC=30,求线段OH的长.
(1)、如图1,求证:∠ABC=2∠CAD;(2)、如图2,延长AD,交⊙O于点E,点F在线段AD上,DF=DE,过点F作FG⊥AC,垂足为点G,求证: AG=CG;(3)、如图3,在(2)的条件下,连接CE,点H在线段BD上,CH=CE,连接AH、OH,若AB=10, S△ABC=30,求线段OH的长.