广东省惠州市六校2023-2024学年高二上学期数学10月联考试卷

试卷更新日期：2023-11-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列说法不正确的是（）

A、直四棱柱是长方体 B、正方体是平行六面体 C、长方体是平行六面体 D、平行六面体是四棱柱

查看试题解析
2. 若 $P (1 ， 0 ， - 2)$ ， $Q (3 ， 1 ， 1)$ 在直线 $l$ 上，则直线 $l$ 的一个方向向量为（）

A、 $(1 ， 2 ， 3)$ B、 $(1 ， 3 ， 2)$ C、 $(2 ， 1 ， 3)$ D、 $(3 ， 2 ， 1)$

查看试题解析
3. 下列关于概率的命题，错误的是（）

A、对于任意事件A ，都有 $P (A) \geq 0$ B、必然事件的概率为1 C、如果事件A与事件B对立，那么一定有 $P (A) + P (B) = 1$ D、若A ， B是一个随机试验中的两个事件，则 $P (A ∪ B) = P (A) + P (B)$

查看试题解析
4. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E ， F ， G ， H$ 分别为 $A_{1} B_{1} ， B_{1} C_{1} ， A_{1} D_{1} ， B B_{1}$ 的中点，则 $| \vec{G F} + \vec{G H} + 2 \vec{E G} | =$ （）

A、 $\sqrt{6}$ B、 $2 \sqrt{6}$ C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
5. 已知向量 $\vec{O A} = (0 ， 1 ， 2) ， \vec{O B} = (- 1 ， 0 ， 1) ， \vec{O C} = (2 ， 1 ， λ)$ ，若 $O ， A ， B ， C$ 共面，则 $\vec{O C}$ 在 $\vec{O B}$ 上的投影向量的模为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
6. 在一个边长为2的等边三角形 $A B C$ 中，若点P是平面 $A B C$ (包括边界)中的任意一点，则 $\vec{P A} \cdot \vec{P C}$ 的最小值是（）

A、 $- \frac{5}{2}$ B、 $- \frac{4}{3}$ C、 $- 1$ D、 $- \frac{3}{4}$

查看试题解析
7. 我们打印用的A4纸的长与宽的比约为 $\sqrt{2}$ ，之所以是这个比值，是因为把纸张对折，得到的新纸的长与宽之比仍约为 $\sqrt{2}$ ，纸张的形状不变．已知圆柱的母线长小于底面圆的直径长（如图所示），它的轴截面ABCD为一张A4纸，若点E为上底面圆上弧AB的中点，则异面直线DE与AB所成的角约为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
8. 如图，在直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = 3$ ，底面ABCD是边长为 $\sqrt{2}$ 的菱形， $∠ A D C = 135 °$ ， $D E ⊥ A B$ 于点E ，建立如图所示的空间直角坐标系 $D - x y z$ ，若点 $P (a + 1 ， - \frac{3}{2} ， \frac{3}{2})$ 在平面 $A_{1} B C_{1}$ 内，则a的值为（）

A、 $- 1$ B、 $\frac{3}{2}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析

二、多选题

9. 设P表示一个点，a ， b表示两条不同直线， $α$ ， $β$ 表示两个不同平面，下列说法不正确的是（）

A、若 $P \in a$ ， $P \in α$ ，则 $a \subset α$ B、若 $a ∩ b = P$ ， $b \subset β$ ，则 $a \subset β$ C、若 $a / / b$ ， $a \subset α$ ， $P \in b$ ， $P \in α$ ，则 $b \subset α$ D、若 $α ∩ β = b$ ， $P \in α$ ， $P \in β$ ，则 $P \in b$

查看试题解析
10. 已知平面非零向量 $\vec{a}$ ， $\vec{b}$ ，下列结论正确的是（）

A、若 ${\vec{a} ， \vec{b}}$ 是平面所有向量的一组基底，且 ${\vec{a} + k \vec{b} ， k \vec{a} + 4 \vec{b}}$ 不是基底，则实数 $k = \pm 2$ B、若存在非零向量 $\vec{c}$ 使得 $\vec{a} \cdot \vec{c} = \vec{b} \cdot \vec{c}$ ，则 $\vec{a} = \vec{b}$ C、若 $| \vec{a} - \vec{b} | = | \vec{a} | + | \vec{b} |$ ，则存在唯一的正实数 $λ$ ，使得 $\vec{b} = λ \vec{a}$ D、设 $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ，且 $\vec{a}$ 与 $\vec{b}$ 不共线，若 $\vec{O P} = \frac{2}{3} \vec{a} + \frac{1}{2} \vec{b}$ ，则 $\frac{S_{△ O P B}}{S_{△ P A B}} = 4$

查看试题解析
11. 在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生大规模群体感染的标准为“连续10天，每天新增疑似病例不超过7人”，过去10天，甲､乙､丙､丁四地新增疑似病例数据信息如下：甲地：平均数为2，众数为2；乙地：中位数为3，极差为4；丙地：平均数为2，中位数为3；丁地：平均数为2，方差为2，甲､乙､丙､丁四地中，一定没有发生大规模群体感染的是（）

A、甲地 B、乙地 C、丙地 D、丁地

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，点E、O分别是 $A_{1} B_{1}$ 、 $A_{1} C_{1}$ 的中点，P在正方体内部且满足 $\vec{A P} = \frac{3}{4} \vec{A B} + \frac{1}{2} \vec{A D} + \frac{2}{3} \vec{A A_{1}}$ ，则下列说法正确的是（）

A、点A到直线BE的距离是 $\frac{2 \sqrt{5}}{5}$ B、点O到平面 $A B C_{1} D_{1}$ 的距离为 $\frac{\sqrt{2}}{4}$ C、平面 $A_{1} B D$ 与平面 $B_{1} C D_{1}$ 间的距离为 $\frac{\sqrt{3}}{3}$ D、点P到直线AB的距离为 $\frac{25}{36}$

查看试题解析

三、填空题

13. 设向量 $\vec{a} = (1 ， 2) ， \vec{b} = (m ， 1)$ ，且 $\vec{b} / / (\vec{a} + \vec{b})$ ，则 $m =$ ．

查看试题解析
14. 某企业为了解员工身体健康情况，采用分层抽样的方法从该企业的销售部门和研发部门抽取部分员工体检，已知该企业销售部门和研发部门的员工人数之比是5：1，且被抽到参加体检的员工中，销售部门的人数比研发部门的人数多84，则参加体检的人数是．

查看试题解析
15. 已知空间向量 $\vec{a}$ 、 $\vec{b}$ 是相互垂直的单位向量，且 $| \vec{c} | = 5$ ， $\vec{c} \cdot \vec{a} = \vec{c} \cdot \vec{b} = 2 \sqrt{2}$ ，则对任意的实数m ， n ， $| \vec{c} - m \vec{a} - n \vec{b} |$ 的最小值是．

查看试题解析
16. 截角四面体是一种半正八面体，可由四面体经过适当的截角，即截去四面体的四个顶点所产生的多面体.如图所示，将棱长为6的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为2的截角四面体，则该截角四面体的外接球表面积为.

查看试题解析

四、解答题

17. “盲盒”是指商家将动漫、影视作品的周边或设计师单独设计出玩偶放入盒子里，当消费者购买这个盒子，因盒子上没有标注，只有打开才会知道抽到什么，不确定的刺激会加强重复决策，从而刺激消费．某商家将编号为1，2，3的三个玩偶随机放入编号为1，2，3的三个盒子里，每个盒子放一个玩偶，每个玩偶的放置是相互独立的．

(1)、共有多少种不同的放法？请列举出来；

(2)、求盒中放置的玩偶的编号与所在盒的编号均不相同的概率．

查看试题解析
18. 某校对参加亚运知识竞赛的100名学生的成绩进行统计，分成 $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ 五组，得到如图所示频率分布直方图．

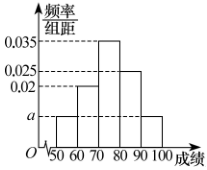(1)、估计该校参加亚运知识竞赛的学生成绩的众数和平均数；

(2)、估计该校参加亚运知识竞赛的学生成绩的80%分位数．

查看试题解析
19. 如图所示，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为平行四边形， $∠ A D C = 45 ° ， A D = A C = 1$ ， O为 $A C$ 的中点， $P O ⊥$ 平面 $A B C D$ ， $P O = 2$ ， M为 $P D$ 的中点．

(1)、证明： $P B / /$ 平面 $A C M$ ；

(2)、求直线 $A M$ 与平面 $A B C D$ 所成角的正切值．

查看试题解析
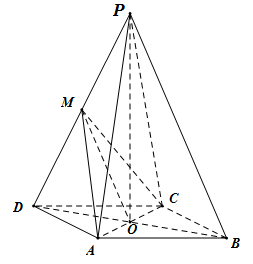20. 小王创建了一个由他和甲、乙、丙共4人组成的微信群，并向该群发红包，每次发红包的个数为1个（小王自己不抢），假设甲、乙、丙3人每次抢得红包的概率相同．

(1)、若小王发2次红包，求甲恰有1次抢得红包的概率；

(2)、若小王发3次红包，其中第1，2次，每次发5元的红包，第3次发10元的红包，求乙抢得所有红包的钱数之和不小于10元的概率．

查看试题解析
21. 已知 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，且 $\frac{a + b - c}{b + c - a} = \frac{1}{9} ， \frac{a + b - c}{c + a - b} = \frac{1}{5}$ .

(1)、若 $∠ A C B$ 的平分线与边 $A B$ 交于点 $D$ ，求 $\frac{A D}{c}$ 的值；

(2)、若 $a = 2$ ，点 $M ， N$ 分别在边 $A C ， B C$ 上， $△ C M N$ 的周长为5，求 $M N$ 的最小值.

查看试题解析
22. 如图，四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面ABCD为直角梯形， $∠ D A B = ∠ A D C = 90 °$ ， $A B = A D = 1$ ， $C D = 2$ ，直线 $B D_{1}$ 与直线CD所成的角取得最大值．点M为 $C D_{1}$ 的中点，且 $C D_{1} = 2 B M$ ．

(1)、证明：平面 $B D M ⊥$ 平面 $B D_{1} M$ ；

(2)、若钝二面角 $B - D M - C$ 的余弦值为 $- \frac{\sqrt{15}}{15}$ ，当 $B D_{1} > B D$ 时，求三棱锥 $D - B D_{1} M$ 的体积．

查看试题解析