浙江省杭金湖四校2023-2024学年高三上学期数学第六次联考试卷
试卷更新日期:2023-11-09 类型:高考模拟
一、单选题
-
1. 已知集合 , 则集合有( )个子集.A、0 B、1 C、2 D、42. 已知向量与直线平行且 , , 则向量在向量方向上的投影向量可以是( )A、 B、 C、 D、3. 已知、满足 , , 则的实部是( )A、 B、 C、 D、4. 函数的大致图象为( )A、
 B、
B、 C、
C、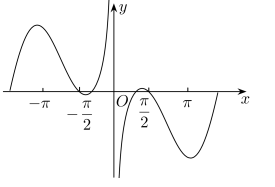 D、
D、 5. “杨辉三角”是中国古代重要的数学成就,如图是由“杨辉三角”拓展而成的三角形数阵,记为图中所选数1,构成的数列的第项,则的值为( )
5. “杨辉三角”是中国古代重要的数学成就,如图是由“杨辉三角”拓展而成的三角形数阵,记为图中所选数1,构成的数列的第项,则的值为( ) A、252 B、426 C、462 D、9246. 锐角满足 , 则下列等式成立的是( )A、 B、 C、 D、7. 已知椭圆的左顶点为A , 右焦点为 , 过右焦点作x轴垂线交椭圆于B、C两点,连结BO并延长交AC于点M , 若M为AC的中点,则椭圆的离心率为( )A、 B、 C、 D、8. 已知 , , 则的最小值为( )A、 B、 C、 D、1
A、252 B、426 C、462 D、9246. 锐角满足 , 则下列等式成立的是( )A、 B、 C、 D、7. 已知椭圆的左顶点为A , 右焦点为 , 过右焦点作x轴垂线交椭圆于B、C两点,连结BO并延长交AC于点M , 若M为AC的中点,则椭圆的离心率为( )A、 B、 C、 D、8. 已知 , , 则的最小值为( )A、 B、 C、 D、1二、多选题
-
9. 某地区高三男生的身高X服从正态分布 , 则( )A、 B、若越大,则越大 C、 D、10. 函数 , 下列说法正确的是( )A、是周期函数 B、最大值是1 C、图像至少有一条对称轴 D、图像至少有一个对称中心11. 已知 , 则下列命题为真命题的是( )A、的取值范围为 B、的取值范围为 C、的取值范围为 D、的取值范围为12. 在空间直角坐标系中,有以下两条公认事实:
①过点 , 且以为方向向量的空间直线l的方程为;
②过点 , 且为法向量的平面的方程为 .
现已知平面 , , , ( )
A、 B、 C、 D、三、填空题
-
13. 已知函数 , 曲线在点处的切线方程是 .14. 用4种不同颜色给一个正四面体涂色,每个面涂一种颜色,4个颜色都要用到,共有种涂色的方法.15. 直线与直线所成夹角大小为 .16. 若正四面体的棱长为3,平面ABC内有一动点P到平面、平面、平面的距离依次成等差数列,则点P在面内的轨迹的长度为.
四、解答题
-
17. 直角三角形ABC斜边上一点D满足 ,
 (1)、求证:;(2)、若 , 求角B的大小.18. 已知数列的前项和为 , 满足 , .(1)、求的通项公式;(2)、若 , 求数列的前20项和.
(1)、求证:;(2)、若 , 求角B的大小.18. 已知数列的前项和为 , 满足 , .(1)、求的通项公式;(2)、若 , 求数列的前20项和.五、证明题
-
19. 如图,在四棱锥中,平面平面ABCD,底面ABCD是直角梯形, , , , .
 (1)、求证:;(2)、若平面平面PBC,且中,AD边上的高为3,求AD的长.
(1)、求证:;(2)、若平面平面PBC,且中,AD边上的高为3,求AD的长.六、解答题
-
20. 随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对某社区随机抽取了5人进行调查,将调查情况进行整理后制成下表:
年龄
[20,25)
[25,30)
[30,35)
[35,40)
[40,45)
人数
4
5
8
5
3
年龄
[45,50)
[50,55)
[55,60)
[60,65)
[65,70)
人数
6
7
3
5
4
年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(1)、求年龄在[25,30)的被调查者中选取的2人都是赞成的概率;(2)、求选中的4人中,至少有3人赞成的概率;(3)、若选中的4人中,不赞成的人数为X , 求随机变量X的分布列和数学期望.七、证明题
-