陕西省西安市灞桥区2023-2024学年高二上学期数学第一次联考试卷
试卷更新日期:2023-11-09 类型:月考试卷
一、单选题
-
1. 直线在轴上的截距为 , 在轴上的截距为 , 则( )A、 , B、 , C、 , D、 ,2. 若 , , 三点共线,则( )A、4 B、 C、1 D、03. 若直线是圆的一条对称轴,则( )A、0 B、1 C、2 D、44. 圆与圆的公切线有( )A、1条 B、2条 C、3条 D、4条5. 如图,在圆锥SO中,AB是底面圆的直径,D , E分别为SO , SB的中点, , , 则直线AD与直线CE所成角的余弦值为( )
 A、 B、 C、 D、6. 若某等腰直角三角形斜边所在直线的倾斜角为 , 则该三角形两条直角边所在直线的斜率之和为( )A、0 B、 C、 D、7. 如图,在正四棱柱中, , . 点 , , 分别在棱 , , 上, , , , 则点到平面的距离为( )
A、 B、 C、 D、6. 若某等腰直角三角形斜边所在直线的倾斜角为 , 则该三角形两条直角边所在直线的斜率之和为( )A、0 B、 C、 D、7. 如图,在正四棱柱中, , . 点 , , 分别在棱 , , 上, , , , 则点到平面的距离为( )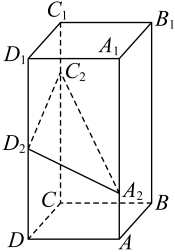 A、 B、 C、 D、8. 如图,在四棱锥中,底面 , 底面是矩形, , , 是的中点, . 若点在矩形内,且平面 , 则( )
A、 B、 C、 D、8. 如图,在四棱锥中,底面 , 底面是矩形, , , 是的中点, . 若点在矩形内,且平面 , 则( )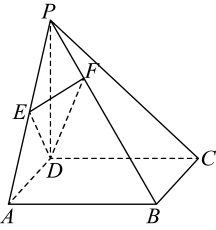 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知直线 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、过定点 D、当时,与之间的距离的最大值为10. 如图,在四棱柱中,四边形ABCD是正方形, , , 且 , 则( )
 A、 B、 C、 D、直线与平面ABCD所成的角为11. 已知直线与圆交于两点,下列说法正确的是( )A、的最小值是4 B、若过点的直线垂直平分弦 , 则 C、的面积的最大值是 D、中点的轨迹方程为12. 清初著名数学家孔林宗曾提出一种“蒺藜形多面体”,其可由两个正交的正四面体组合而成,如图1,也可由正方体切割而成,如图2.在图2所示的“蒺藜形多面体”中,若 , 则给出的说法中正确的是( )
A、 B、 C、 D、直线与平面ABCD所成的角为11. 已知直线与圆交于两点,下列说法正确的是( )A、的最小值是4 B、若过点的直线垂直平分弦 , 则 C、的面积的最大值是 D、中点的轨迹方程为12. 清初著名数学家孔林宗曾提出一种“蒺藜形多面体”,其可由两个正交的正四面体组合而成,如图1,也可由正方体切割而成,如图2.在图2所示的“蒺藜形多面体”中,若 , 则给出的说法中正确的是( ) A、该几何体的表面积为 B、该几何体的体积为4 C、二面角的余弦值为 D、若点P , Q在线段BM , CH上移动,则PQ的最小值为
A、该几何体的表面积为 B、该几何体的体积为4 C、二面角的余弦值为 D、若点P , Q在线段BM , CH上移动,则PQ的最小值为三、填空题
-
13. 若向量 , , 且 , 则 .14. 如图,圆和圆的圆心分别为 , , 半径都为 , 写出一条与圆和圆都相切的直线的方程:.
 15. 在正四棱台中, , , , , , 若平面 , 则 .
15. 在正四棱台中, , , , , , 若平面 , 则 .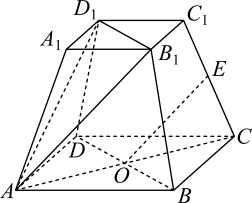
四、双空题
-
16. 已知为圆上的动点,点在轴上,若 , 则点的坐标为;若点为直线上的动点,则的最小值为.
五、解答题
-
17. 已知的三个顶点的坐标分别为 , , .(1)、求点到直线的距离;(2)、求边上的高所在直线的方程.18. 如图,在直四棱柱中, , , , E , F , G分别为棱 , , 的中点.
 (1)、求的值;(2)、证明:C , E , F , G四点共面.19. 如图,在正方体中,E , F , G分别是 , , 的中点.
(1)、求的值;(2)、证明:C , E , F , G四点共面.19. 如图,在正方体中,E , F , G分别是 , , 的中点. (1)、证明: .(2)、求直线与平面所成角的正弦值.
(1)、证明: .(2)、求直线与平面所成角的正弦值.
-
