云南省昆明市五华区2024届高三上学期数学期中试卷

试卷更新日期：2023-11-09 类型：期中考试

进入出卷网下载

一、单选题

1. 设集合 $M = {x | - 3 \leq x \leq 0}$ ， $N = {x | x^{2} \leq 1}$ ，则 $M \cap N =$ （）

A、 ${0}$ B、 ${- 1 ， 0}$ C、 $(- 1 ， 0)$ D、 $[- 1 ， 0]$

查看试题解析
2. $\frac{i}{3 + 4 i} =$ （）

A、 $\frac{4}{5} + \frac{3}{5} i$ B、 $\frac{4}{5} - \frac{3}{5} i$ C、 $\frac{4}{25} + \frac{3}{25} i$ D、 $- \frac{4}{25} + \frac{3}{25} i$

查看试题解析
3. 已知甲、乙两个班的学生人数分别为45人和55人，在某次考试中，甲、乙两个班的数学平均分分别为110分和90分，则这两个班全体学生的平均分为（）

A、98分 B、99分 C、100分 D、101分

查看试题解析
4. 已知 ${a_{n}}$ 为等差数列，数列 ${b_{n}}$ 满足： $a_{n} b_{n} = 2 n^{2} - n (n \in N^{*})$ ，若 $5 a_{4} = 7 a_{3}$ ，且 $a_{1} + b_{1} = 2$ ，则 $a_{9} + b_{10} =$ （）

A、26 B、27 C、28 D、29

查看试题解析
5. 工厂需要将某种废气经过过滤后排放，已知该废气的污染物含量 $P$ （单位： $m g / L$ ）与过滤时间 $t$ （单位： $h$ ）的关系为 $P = P_{0} e^{- 0.02 t}$ （ $P_{0}$ 为污染物的初始含量），则污染物减少到初始含量的 $20 %$ 大约需要（参考数据： $l n 5 \approx 1.6$ ）（）

A、 $60 h$ B、 $70 h$ C、 $80 h$ D、 $90 h$

查看试题解析
6. 已知函数 $f (x) = x^{3} - 2 a x^{2} + a^{2} x + 1$ 在 $x = 1$ 处有极小值，则 $a$ 的值为（）

A、1 B、3 C、1或3 D、 $- 1$ 或3

查看试题解析
7. 已知 $A (- 2 ， 3) ， B (a ， 0)$ ，若直线 $A B$ 关于 $x$ 轴对称的直线与圆 $(x - 3)^{2} + (y - 2)^{2} = 1$ 有公共点，则 $a$ 的取值范围是（）

A、 $[\frac{1}{4} ， 2]$ B、 $(- \infty ， \frac{1}{4}] ∪ [2 ， + \infty)$ C、 $[\frac{1}{2} ， 4]$ D、 $(- \infty ， \frac{1}{2}] ∪ [4 ， + \infty)$

查看试题解析
8. 已知 $α ， β \in (- \frac{π}{4} ， \frac{π}{4})$ ， $c o s (2 α + 2 β) = - \frac{7}{9}$ ， $s i n α s i n β = \frac{1}{4}$ ，则 $c o s (α - β) =$ （）

A、 $- \frac{1}{6}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{5}{6}$

查看试题解析

二、多选题

9. 一项比赛共有9位评委，选手完成比赛后，每位评委现场给出一个“初始评分”，去掉一个最高分，去掉一个最低分，剩余7位评委的评分为“有效评分”．则下列叙述一定正确的是（）

A、同一个选手的“初始评分的中位数等于”有效评分的中位数 B、同一个选手的“初始评分”的下四分位数等于“有效评分”的下四分位数 C、同一个选手的“初始评分”的平均数不低于“有效评分”的平均数 D、同一个选手的“初始评分”的方差不低于“有效评分”的方差

查看试题解析
10. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 棱长为2，直线 $A C_{1}$ 与平面 $A_{1} B D$ 交于点 $P ， Q$ 为线段 $B D$ 上的动点，则（）

A、当 $Q$ 为 $B D$ 中点时， $A_{1} ， P ， Q$ 三点共线 B、存在点 $Q$ ，使 $A Q ⊥ A_{1} C_{1}$ C、直线 $P Q$ 与 $A C_{1}$ 的夹角为 $60 °$ D、四面体 $B_{1} C D_{1} Q$ 的体积为定值

查看试题解析
11. 已知 $O$ 为坐标原点，点 $A (2 ， 2)$ 在抛物线 $C ： y^{2} = 2 p x (p > 0)$ 上，经过点 $B (2 ， 0)$ 且斜率大于零的直线交 $C$ 于 $P ， Q$ 两点，点 $P$ 在第一象限，则（）

A、 $C$ 的准线为 $x = - 1$ B、以 $P Q$ 为直径的圆经过原点 C、 $S_{△ O P Q} > 2 S_{△ O A B}$ D、 $∠ O A P + ∠ O Q B > 180 °$

查看试题解析
12. 已知函数 $f (x)$ 的定义域为 $R$ ，对于任意的 $x ， y \in R$ ，都有 $f (x + y) + f (x - y) = 2 f (x) f (y)$ 成立，则（）

A、 $f (0) = 0$ B、若 $f (1) = 1$ ，则 $f (2) = 1$ C、 $f (x)$ 一定是偶函数 D、若 $f (1) = 0$ ，则 $f (1) + f (2) + f (3) + f (4) + ⋯ + f (2024) = 0$

查看试题解析

三、填空题

13. 函数 $f (x) = s i n 2 x + c o s 2 x$ 在 $[0 ， \frac{π}{2}]$ 上的最大值是．

查看试题解析
14. 第19届亚洲运动会于2023年9月23日10月8日在我国杭州成功举办，中国国家队以201金、111银、71铜的优异成绩位列奖牌榜榜首．此次亚运会的颁奖花束——“硕果累累”，由花材和花器两部分组成，如图1．其中花器的造型灵感来自中国南宋时期官窑花解，由国家级非物质文化遗产东阳木雕制作而成，可以近似看作由大、小两个圆台拼接而成的组合体，如图2．已知大圆台的两底面半径和高分别为 $2 c m 、 4 c m 、 12 c m$ ，小圆台的两底面半径和高分别为 $2 c m 、 3 c m 、 6 c m$ ，则该几何体的体积为 $c m^{3}$ ．

查看试题解析
15. 向量 $\vec{a} = (- 2 ， 1)$ 在向量 $\vec{b}$ 上的投影向量为 $\frac{1}{2} \vec{b}$ ，则 $| \vec{b} |$ 的最大值为．

查看试题解析
16. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的两个焦点为 $F_{1} (- c ， 0) ， F_{2} (c ， 0) (c > 0)$ ，过 $F_{1}$ 作倾斜角为 $\frac{π}{4}$ 的直线交椭圆于 $A ， B$ 两点，若 $△ A B F_{2}$ 的内切圆半径 $r = \frac{\sqrt{2}}{6} c$ ，则该椭圆的离心率为．

查看试题解析

四、解答题

17. 图1是由正方形 $A B C D$ 和正三角形 $A D E$ 组成的一个平面图形，将 $△ A D E$ 沿 $A D$ 折起，使点 $E$ 到达点 $P$ 的位置， $Q$ 为 $P C$ 的中点，如图2．

(1)、求证： $A P$ $/ /$ 平面 $Q B D$ ；

(2)、若平面 $P A D ⊥$ 平面 $A B C D$ ，求平面 $P A D$ 与平面 $Q B D$ 夹角的余弦值．

查看试题解析
18. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，已知 $2 S_{n} = 3 a_{n} - 3 (n \in N^{*})$ ．

(1)、求 $a_{n}$ ；

(2)、若 $b_{n} = \frac{1}{a_{n}} + l o g_{3} a_{2 n - 1}$ ，记 $T_{n}$ 为 ${b_{n}}$ 的前 $n$ 项和，且满足 $T_{n} < 150$ ，求 $n$ 的最大值．

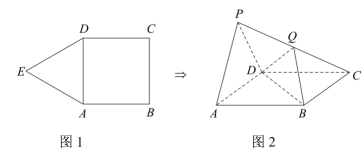查看试题解析
19. $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c ， A D$ 平分 $∠ B A C$ 且交 $B C$ 于点 $D$ ．已知 $A D = 1 ， △ A C D$ 的面积为1．

(1)、若 $∠ B A C = \frac{π}{2}$ ，求 $C D$ ；

(2)、若 $C D = 2 B D$ ，求 $t a n ∠ B A C$ ．

查看试题解析
20. 甲、乙两人玩一种游戏，游戏规则如下：放置一张纸片在地面指定位置，其中一人在固定位置投篮，若篮球被篮板反弹后击中纸片，则本次游戏成功，此人继续投篮，否则游戏失败，换为对方投篮．已知第一次投篮的人是甲、乙的概率分别为 $\frac{2}{3}$ 和 $\frac{1}{3}$ ，甲、乙两人每次游戏成功的概率分别为 $\frac{7}{10}$ 和 $\frac{4}{5}$ ．

(1)、求第2次投篮的人是甲的概率；

(2)、记第 $n$ 次投篮的人是甲的概率为 $P_{n}$ ，
⑴用 $P_{n}$ 表示 $P_{n + 1}$ ；
⑵求 $P_{n}$ ．

查看试题解析
21. 设 $A ， B$ 两点的坐标分别为 $(- 2 ， 0) ， (2 ， 0)$ ，直线 $A M ， B M$ 相交于点 $M$ ，且它们的斜率之积是 $\frac{1}{4}$ ，记点 $M$ 的轨迹为 $C$ ．

(1)、求 $C$ 的方程；

(2)、若 $T$ 为直线 $x = 1$ 上的一动点，直线 $A T ， B T$ 分别与 $C$ 交于点 $P ， Q$ ．求证：直线 $P Q$ 过定点．

查看试题解析
22. 已知函数 $f (x) = x^{2} l n x + a x ， g (x) = x e^{x} + x s i n x$ ，其中 $a \in R$ ．

(1)、若 $f (x)$ 为增函数，求 $a$ 的取值范围；

(2)、若 $a = 1$ ，证明： $g (x) > f (x)$ ．

查看试题解析