备考2024年浙江中考数学一轮复习专题5.3因式分解模拟集训

试卷更新日期：2023-11-07 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列等式从左到右变形，属于因式分解的是（）

A、 $x + 2 y = (x + y) + y$ B、 $p (q + h) = p q + p h$ C、 $5 x^{2} y - 10 x y^{2} = 5 x y (x - 2 y)$ D、 $4 a^{2} - 4 a + 1 = 4 a (a - 1) + 1$

查看试题解析
2. 分解因式 ${(x - 1)}^{2} - 2 (x - 1) + 1$ 的结果是（）

A、 $(x - 1) (x - 2)$ B、 $x^{2}$ C、 ${(x + 1)}^{2}$ D、 ${(x - 2)}^{2}$

查看试题解析
3. 下列因式分解正确的是（）

A、x²+y²=（x+y） B、x²+2xy+y²=（x-y）² C、x²+x=x（x-1） D、x²-y²=（x+y）（x-y）

查看试题解析
4. 下列各式中，能用平方差公式分解因式的是（）

A、 $x^{2} + 4 y^{2}$ B、 $- x^{2} + 4 y^{2}$ C、 $x^{2} - 2 y + 1$ D、 $- x^{2} - 4 y^{2}$

查看试题解析
5. 把多项式 $a^{2} - 9 a$ 分解因式，结果正确的是（）

A、 $a (a - 9)$ B、 $(a + 3) (a - 3)$ C、 $a (a + 3) (a - 3)$ D、 $- a (a - 9)$

查看试题解析
6. 如果 $x^{3} + a x^{2} + b x + 8$ 能被 $x^{2} + 3 x + 2$ 整除，则 $\frac{b}{a}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、3 D、 $\frac{1}{3}$

查看试题解析
7. 若 $x^{2} + y^{2} = 1$ ，则 $\sqrt{x^{2} - 4 x + 4} + \sqrt{x y - 3 x + y - 3}$ 的值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 下列语句中，其中正确的个数是（）
①将多项式a（x﹣y）²﹣b（y﹣x）因式分解，则原式＝（x﹣y）（ax﹣ay+b）；②将多项式x²+4y²﹣4xy因式分解，则原式＝（x﹣2y）²；③90°的圆周角所对的弦是直径；④半圆（或直径）所对的圆周角是直角．

A、1 B、2 C、3 D、4

查看试题解析
9. 如果多项式 $p = a^{2} + 2 b^{2} + 2 a + 4 b + 1008$ ，则p的最小值是（）

A、1005 B、1006 C、1007 D、1008

查看试题解析
10. 已知 $M = a^{2} + 4 b^{2} ， N = 4 a b$ （ $a ， b$ 为任意有理数），则M与N的大小关系是（）

A、M>N B、M<N C、M ≥N D、M ≤ N

查看试题解析

二、填空题

11. 已知 $x - y = \frac{1}{2}$ ， $x y = \frac{4}{3}$ ，则 $x y^{2} - x^{2} y$ 的值是.

查看试题解析
12. 分解因式： $a^{2} + 4 a b + 4 b^{2} =$ ．

查看试题解析
13. 因式分解： $x^{2} - 8 x + 16 =$ ．

查看试题解析
14. 把多项式2x²－2分解因式的结果是．

查看试题解析
15. 已知 $a b = 3$ ， $a + b = 4$ ，则代数式 $a^{3} b + a b^{3}$ 的值为．

查看试题解析
16. 已知 $5^{4} - 1$ 能被 $20 ~ 30$ 之间的两个整数整除，则这两个整数是.

查看试题解析

三、计算题

17. 计算：

(1)、分解因式： $a^{2} - 4 a + 4$ ；

(2)、解分式方程： $\frac{x}{2 - x} - \frac{1}{x - 2} = 3$

查看试题解析

四、综合题

18. 观察两个连续偶数的平方差：
①4²-2²=12，②6²-4²=20，③8²-6²=28，.... ....

(1)、写出第n个等式，并进行证明；

(2)、问172是否可以写成两个连续偶数的平方差?如果能，请写出这两个偶数：如果不能，请说明理由.

查看试题解析
19. 如图，C为线段AB上一点，AC＝4，BC＝2，射线CD⊥AB于点C，P为射线CD上一点，连接PA，PB.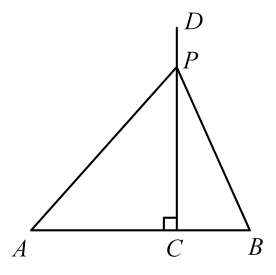

【发现、提出问题】 ①当PC＝3时，求PA²－PB²的值；

②小亮发现PC取不同值时，PA²－PB²的值存在一定规律，请猜想该规律 .

【分析、解决问题】请证明你的猜想.

【运用】当PA－PB＝1时，△PAB的周长为 .

查看试题解析

20. 因式分解

{(3 x + y)}^{2} - {(x + 3 y)}^{2}

.小禾因式分解后，通过代入特殊值检验时，发现左右两边的值不相等.下面是他的解答和检验过程，请认真阅读并完成相应的任务.

小禾的解法： $(3 x + y)^{2} - (x + 3 y)^{2}$

$= (3 x + y + x + 3 y) (3 x + y - x + 3 y)$ ①

$= (4 x + 4 y) (2 x + 4 y)$ ②

$= 8 (x + y) (x + 2 y)$ ③

小禾的检验：当 $x = 0 ， y = 1$ 时，

$(3 x + y)^{2} - (x + 3 y)^{2}$

$= 1^{2} - 3^{2}$

$= - 1 - 9$

$= - 8$

∵ $- 8 \neq 16$

∴分解因式错误.

$8 (x + y) (x + 2 y)$

$= 8 \times 1 \times 2$

$= 16$

任务：

(1)、小禾的解答是从第几步开始出错的，并帮助他指出错误的原因.

(2)、请尝试写出正确的因式分解过程.

查看试题解析

21. 对于任意一个四位数，我们可以记为 $\bar{abcd}$ ，即 $\bar{abcd} = 1000 a + 100 b + 10 c + d .$ 若规定：对四位正整数 $\bar{abcd}$ 进行 $F$ 运算，得到整数 $F (\bar{abcd}) = a^{4} + b^{3} + c^{2} + d^{1} .$ 例如， $F (1249) = 1^{4} + 2^{3} + 4^{2} + 9^{1} = 34$ ； $F (2020) = 2^{4} + 0^{3} + 2^{2} + 0^{1} = 20$ .

(1)、计算： $F (2137)$ ；

(2)、当 $c = e + 2$ 时，证明： $F (\bar{abcd}) - F (\bar{abed})$ 的结果一定是4的倍数；

(3)、求出满足 $F (\bar{32 xy}) = 98$ 的所有四位数.

查看试题解析
22. 对于一个各个数位上的数字均不为零的三位正整数n，如果它的百位数字、十位数字、个位数字是由依次增加相同的非零数字组成，则称这个三位数为“递增数”，记为D（n），把这个“递增数”的百位数字与个位数字交换位置后，得到321，即E（123）=321，规定F（n）= $\frac{E (n) - D (n)}{198}$ ，如F（123）= $\frac{321 - 123}{198}$ =1.

(1)、计算：F（159），F（246）；

(2)、若D（s）是百位数字为1的数，D（t）是个位数字为9的数，且满足
F（s）+F（t）=5，记k= $\frac{2 D (s) + D (t)}{9}$ ，求k的最大值.

查看试题解析

备考2024年浙江中考数学一轮复习专题5.3因式分解 模拟集训

一、选择题

二、填空题

三、计算题

四、综合题

备考2024年浙江中考数学一轮复习专题5.3因式分解模拟集训