备考2024年浙江中考数学一轮复习专题5.2因式分解 真题集训

试卷更新日期：2023-11-07 类型：一轮复习

进入 出卷网 下载

一、选择题

  • 1. 分解因式：4a2−1=（    ）
    A、(2a−1)(2a+1) B、(a−2)(a+2) C、(a−4)(a+1) D、(4a−1)(a+1)

    查看试题解析

  • 2. 要使式子 −7ab−14abx+49aby=−7ab( ) 成立，则“（ ）"内应填的式子是（ ）
    A、−1+2x+7y B、−1−2x+7y C、1−2x−7y D、1+2x−7y

    查看试题解析

  • 3. 下列多项式中，能运用平方差公式分解因式的是（   ）
    A、a2+b2 B、2a−b2 C、a2−b2 D、−a2−b2

    查看试题解析

  • 4. 把代数式2x2﹣18分解因式，结果正确的是（   ）
    A、2（x2﹣9） B、2（x﹣3）2 C、2（x+3）（x﹣3） D、2（x+9）（x﹣9）

    查看试题解析

  • 5. 下列各式能用完全平方公式进行分解因式的是（   ）

    A、x2+1 B、x2+2x﹣1 C、x2+x+1 D、x2+4x+4

    查看试题解析

  • 6. 若 a = 2 ， a − 2 b = 3 ，则 2 a 2 − 4 a b 的值为（   ）
    A、2 B、4 C、6 D、12

    查看试题解析

  • 7. 多项式 (x+2)(2x−1)−2(x+2) 可以因式分解成 (x+m)(2x+n) ，则 m−n 的值是（   ）
    A、3 B、0 C、5 D、1

    查看试题解析

  • 8. 因式分解： 1−4y2 =（   ）
    A、(1−2y)(1+2y) B、(2−y)(2+y) C、(1−2y)(2+y) D、(2−y)(1+2y)

    查看试题解析

  • 9. 设a，b是实数，定义@的一种运算如下：a@b=（a+b）2﹣（a﹣b）2 ， 则下列结论：

    ①若a@b=0，则a=0或b=0

    ②a@（b+c）=a@b+a@c

    ③不存在实数a，b，满足a@b=a2+5b2

    ④设a，b是矩形的长和宽，若矩形的周长固定，则当a=b时，a@b最大．

    其中正确的是（  ）

    A、②③④ B、①③④ C、①②④ D、①②③

    查看试题解析

  • 10. 把多项式2x2﹣8分解因式，结果正确的是（　　）

    A、2（x2﹣8） B、2（x﹣2）2   C、2（x+2）（x﹣2）   D、2x（x﹣4x）

    查看试题解析

二、填空题

  • 11. 分解因式：2a2−2a=。

    查看试题解析

  • 12. 一个多项式，把它因式分解后有一个因式为(x+1) ， 请你写出一个符合条件的多项式：。

    查看试题解析

  • 13. 分解因式： m2+4m+4 ＝ ．

    查看试题解析

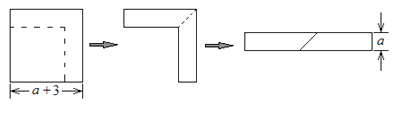
  • 14. 把多项式 x2−3x 因式分解，正确的结果是 ．

    查看试题解析

  • 15.

    如图，从边长为 (a+3) 的正方形纸片中剪去一个边长为3的正方形，剩余部分沿虚线又剪拼成一个如图所示的长方形（不重叠，无缝隙），则拼成的长方形的另一边长是

    查看试题解析

  • 16. 分解因式：4−4x+x2= ．

    查看试题解析

  • 17. 若整式x2+ky2（k为不等于零的常数）能在有理数范围内因式分解，则k的值可以是（写出一个即可）．

    查看试题解析

三、计算题

四、解答题

  • 20. 设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4x2﹣y2）+3x2（4x2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．

    查看试题解析

  • 21. 观察下面的等式：32−12=8×1 ， 52−32=8×2 ， 72−52=8×3 ， 92−72=8×4 ， ⋯
    (1)、写出192−172的结果．
    (2)、按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）
    (3)、请运用有关知识，推理说明这个结论是正确的．

    查看试题解析