(人教版)2023-2024学年九年级数学上册 25.2 用列举法求概率 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次,若n次抛掷所出现的向上一面的点数之和大于n2 , 则算过关;否则,不算过关.能过第二关的概率是( ).A、 B、 C、 D、2. 甲乙两人轮流在黑板上写下不超过
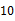 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A、10 B、9 C、8 D、63. 如图有四个转盘,其中C,D转盘分成8等分.让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( ).A、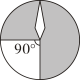 B、
B、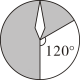 C、
C、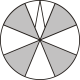 D、
D、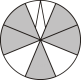 4. 甲、乙两人掷两个普通的立方体骰子,若掷出的点数之和为7,则甲赢;若掷出的点数之和为8,则乙赢.这个游戏规则( ).A、公平 B、对甲有利 C、对乙有利 D、无法判断5. 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( ).A、 B、 C、 D、6. 如图所示,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ).
4. 甲、乙两人掷两个普通的立方体骰子,若掷出的点数之和为7,则甲赢;若掷出的点数之和为8,则乙赢.这个游戏规则( ).A、公平 B、对甲有利 C、对乙有利 D、无法判断5. 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( ).A、 B、 C、 D、6. 如图所示,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ). A、 B、 C、 D、7. 从标有数字0,2,4,6的四张牌中任意抽出两张,所得牌上的数字之和最可能是( ).A、2 B、4 C、6 D、88. 在1,2,3,4四个数中,随机抽取两个不同的数,其乘积大于4的概率为( )A、 B、 C、 D、9. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( )
A、 B、 C、 D、7. 从标有数字0,2,4,6的四张牌中任意抽出两张,所得牌上的数字之和最可能是( ).A、2 B、4 C、6 D、88. 在1,2,3,4四个数中,随机抽取两个不同的数,其乘积大于4的概率为( )A、 B、 C、 D、9. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( ) A、 B、 C、 D、10. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分若从这四部著作中(随机抽取两本先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( )
A、 B、 C、 D、10. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分若从这四部著作中(随机抽取两本先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是.
12. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为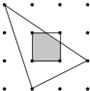 13. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为 .
13. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为 .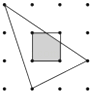 14. 小红、小芳、小明在一起做游戏,他们约定用“石头、剪刀、布”的方式确定做游戏的先后顺序.在一个回合中,三个人都出“布”的概率是 .15. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块正方形地砖的大小、质地完全相同,那么该小球停留在白色区域的概率是
14. 小红、小芳、小明在一起做游戏,他们约定用“石头、剪刀、布”的方式确定做游戏的先后顺序.在一个回合中,三个人都出“布”的概率是 .15. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块正方形地砖的大小、质地完全相同,那么该小球停留在白色区域的概率是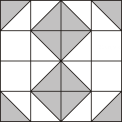
三、解答题
-
16. 四张背面完全相同的纸牌,正面分别写有四个不同的条件,小明将这四张纸牌背面朝上洗匀后,先随机抽出一张(不放回),再随机抽出一张.
 (1)、写出两次摸牌出现的所有可能的结果(用①,②,③,④表示).(2)、以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.17. 某大学组织志愿者周末到社区进行党史学习宣讲,决定通过抽签的方式从A,B,C,D四名志愿者中确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同且不透明的卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字.(1)、“A志愿者被选中”是(填“随机”或“不可能”或“必然”)事件.(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A,B两名志愿者被选中的概率.18. 小明和小刚用如图所示的两个均分的转盘做“配紫色”游戏,游戏规则:分别任意旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.若配成紫色则小刚获胜,否则小明获胜.
(1)、写出两次摸牌出现的所有可能的结果(用①,②,③,④表示).(2)、以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.17. 某大学组织志愿者周末到社区进行党史学习宣讲,决定通过抽签的方式从A,B,C,D四名志愿者中确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同且不透明的卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字.(1)、“A志愿者被选中”是(填“随机”或“不可能”或“必然”)事件.(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A,B两名志愿者被选中的概率.18. 小明和小刚用如图所示的两个均分的转盘做“配紫色”游戏,游戏规则:分别任意旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.若配成紫色则小刚获胜,否则小明获胜.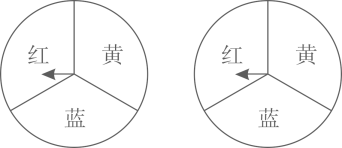 (1)、请用列表或画树状图的方法求出小明获胜的概率.(2)、这个游戏对双方公平吗?请说明理由.19. 一个不透明的袋子中只装有1个红球和2个白球,它们除颜色外其余均相同.现随机从袋子中摸出两个球.(1)、用画树状图或列表的方法求摸出的球恰好颜色不同的概率.(2)、现再将n个红球放入袋中,搅匀后,使摸出1个球是红球的概率为.求n的值.
(1)、请用列表或画树状图的方法求出小明获胜的概率.(2)、这个游戏对双方公平吗?请说明理由.19. 一个不透明的袋子中只装有1个红球和2个白球,它们除颜色外其余均相同.现随机从袋子中摸出两个球.(1)、用画树状图或列表的方法求摸出的球恰好颜色不同的概率.(2)、现再将n个红球放入袋中,搅匀后,使摸出1个球是红球的概率为.求n的值.四、综合题
-
20. 在阳光大课间活动中,某校开展了立定跳远、实心球、长跑等体育活动,为了了解九年一班学生的立定跳远成绩的情况,对全班学生的立定跳远测试成绩进行统计,并绘制了以下不完整的频数分布直方图和扇形图,根据图中信息解答下列问题.
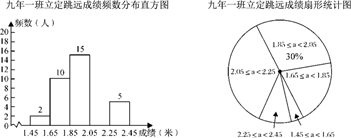 (1)、求九年一班学生总人数,并补全频数分布直方图(标注频数);(2)、求2.05≤a<2.25成绩段在扇形统计图中对应的圆心角度数;(3)、直接写出九年一班学生立定跳远成绩的中位数所在的成绩段;(4)、九年一班在2.25≤a<2.45成绩段中有男生3人,女生2人,现要从这5人中随机抽取2人参加学校运动会,请用列表法或树状图法求出恰好抽到一男一女的概率.21. 有甲乙两个不透明的布袋,甲布袋装有2个形状和重量完全相同的小球,分别标有数字1和2;乙布袋装有3个形状和重量完全相同的小球,分别标有数字﹣3,﹣1和0.先从甲布袋中随机取出一个小球,将小球上标有的数字记作x;再从乙布袋中随机取出一个小球,再将小球标有的数字记作y.(1)、用画树状图或列表法写出两次摸球的数字可能出现的所有结果;(2)、若从甲、乙两布袋中取出的小球上面的数记作点的坐标(x,y),求点(x,y)在一次函数y=﹣2x+1图象上的概率是多少?22. 为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽鄂尔多斯”的号召,康巴什区某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)、求九年一班学生总人数,并补全频数分布直方图(标注频数);(2)、求2.05≤a<2.25成绩段在扇形统计图中对应的圆心角度数;(3)、直接写出九年一班学生立定跳远成绩的中位数所在的成绩段;(4)、九年一班在2.25≤a<2.45成绩段中有男生3人,女生2人,现要从这5人中随机抽取2人参加学校运动会,请用列表法或树状图法求出恰好抽到一男一女的概率.21. 有甲乙两个不透明的布袋,甲布袋装有2个形状和重量完全相同的小球,分别标有数字1和2;乙布袋装有3个形状和重量完全相同的小球,分别标有数字﹣3,﹣1和0.先从甲布袋中随机取出一个小球,将小球上标有的数字记作x;再从乙布袋中随机取出一个小球,再将小球标有的数字记作y.(1)、用画树状图或列表法写出两次摸球的数字可能出现的所有结果;(2)、若从甲、乙两布袋中取出的小球上面的数记作点的坐标(x,y),求点(x,y)在一次函数y=﹣2x+1图象上的概率是多少?22. 为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽鄂尔多斯”的号召,康巴什区某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.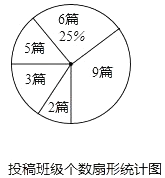
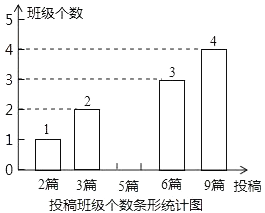 (1)、扇形统计图中投稿篇数为3所对应的扇形的圆心角的度数是;该校八,九年级各班在这一周内投稿的平均篇数是 , ;并将该条形统计图补充完整 .
(1)、扇形统计图中投稿篇数为3所对应的扇形的圆心角的度数是;该校八,九年级各班在这一周内投稿的平均篇数是 , ;并将该条形统计图补充完整 .
(2)、如果要求该校八、九年级的投稿班级个数为30个,估计投稿篇数为5篇的班级个数.
(3)、在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个班级中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
23. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: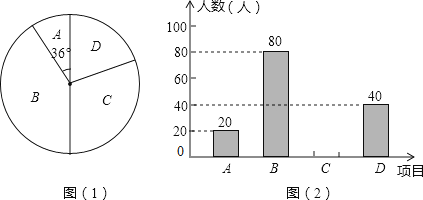 (1)、这次被调查的学生共有 人;
(1)、这次被调查的学生共有 人;
(2)、请你将条形统计图(2)补充完整;
(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答)