（人教版）2023-2024学年九年级数学上册 25.1 随机事件与概率同步分层训练（培优卷）

试卷更新日期：2023-11-07 类型：同步测试

进入出卷网下载

一、选择题

1. 准备两张大小一样，分别画有不同图案的正方形纸片，把每张纸都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图的概率是（）.

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
2. 分別写有数字 $0 ， - 3 ， - 4 ， 2 ， 5$ 的五张卡片.除数字不同外其他均相同，从中任抽一张，那么抽到非负数的概率是（）.

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 某天，气象台预报明天降雨的概率是 $90 %$ ，则下列判断中，正确的是（）.

A、明天一定会下雨 B、明天有 $90 %$ 的地区会降雨 C、明天有 $90 %$ 的时间会下雨 D、明天下雨的可能性很大

查看试题解析
4. 一个盒子中有 $m$ 个红球、8个白球、 $n$ 个黑球，每个球除颜色外其他都相同.从中任取一个球，如果取得的球是白球的概率与不是白球的概率相同，那么 $m$ 与 $n$ 的关系是（）.

A、 $m = 3 ， n = 5$ B、 $m = n = 4$ C、 $m + n = 4$ D、 $m + n = 8$

查看试题解析
5. 如图所示，在平面直角坐标系中，点 $A_{1} ， A_{2}$ 在 $x$ 轴上，点 $B_{1} ， B_{2}$ 在 $y$ 轴上，坐标分别为 $A_{1} (1 ， 0) ， A_{2} (2 ， 0) ， B_{1} (0 ， 1 ），$ $B_{2} (0 ， 2)$ ，分别以 $A_{1} ， A_{2} ， B_{1} ， B_{2}$ 四点中的任意两点与点 $O$ 为顶点作三角形.则所作的三角形为等腰三角形的概率是（）.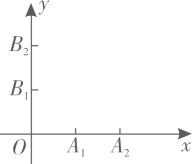

A、 $\frac{3}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 在 $□ A B C D$ 中，AC，BD是两条对角线，现从①AB=BC、②AC=BD、③AC $⊥ B D$ 、④ $A B ⊥ B C$ 中随机取出一个作为条件，即可推出 $□ A B C D$ 是菱形的概率为（）.

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
7. 如图所示，在 $4 \times 4$ 的正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（）.

A、 $\frac{6}{13}$ B、 $\frac{5}{13}$ C、 $\frac{4}{13}$ D、 $\frac{3}{13}$

查看试题解析
8. 下列事件为随机事件的是（）

A、太阳从东方升起 B、你将长到 $5 m$ 高 C、正常情况下，气温低于0 $° C$ 时水结冰 D、抛掷一个均匀的硬币，正面朝上

查看试题解析
9. 在一个不透明的袋子里装有红球6个、黄球4个，这些球除颜色外都相同．小明从袋子中摸一次，摸到黄球的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{3}$ D、 $\frac{3}{10}$

查看试题解析
10. 从长度为3、5、7、8的四条线段中任意选三条组成三角形，其中能组成含有 $60 °$ 角的三角形的概率为（）

A、0.8 B、0.6 C、0.5 D、0.4

查看试题解析

二、填空题

11. 有四张正面分别标有数字-3，0，1，5的不透明卡片，它们除数字不同外其余均相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使关于x的分式方程 $\frac{1 - a x}{x - 2} + 2 = \frac{1}{2 - x}$ 有正整数解的概率为

查看试题解析
12. 有四张正面分别标有数字﹣4，﹣3，﹣2，1，的不透明卡片，它们除数字不同外其他全部相同，现将它们背面朝上，洗匀后从中抽取一张，将该卡片上的数字记为a，放回后洗匀，再从中抽取一张，将该卡片上的数字记为b，则a，b使得二次函数y＝x²﹣（a+5）x+3当x≤1时y随x的增大而减小，且一元二次方程（a+2）x²+bx+1＝0有解的概率为．

查看试题解析
13. 在一个木制的棱长为3的正方体的表面涂上颜色，将它的棱三等分，然后从等分点把正方体锯开，得到27个棱长为l的小正方体，将这些小正方体充分混合后，装入口袋，从这个口袋中任意取出一个小正方体，则这个小正方体的表面恰好涂有两面颜色的概率是.

查看试题解析
14. 如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为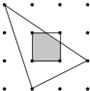

查看试题解析
15. 如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为．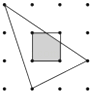

查看试题解析

三、解答题

16. 某市体育中考现场考试内容有三项：50米跑为必测项目；另外在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项．假设每名考生在两项选择项目中任意各选一项，有多少种不同的选择方案？它们都是什么事件？

查看试题解析
17. 下面第一排表示了十张扑克牌中不同情况，任意摸一张，请你用第二排的语言来描述摸到红色扑克牌的可能性大小，并用线连起来．

查看试题解析
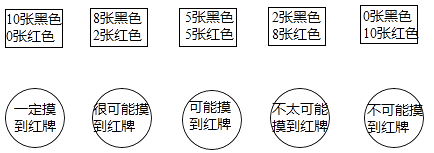18. 在一个不透明的口袋中装有3个带号码的球，球号分别为2，3，4，这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏，游戏规则如下：
先由甲同学从中随机摸出一球，记下球号，并放回搅匀，再由乙同学从中随机摸出一球，记下球号。将甲同学摸出的球号作为一个两位数的十位上的数，乙同学的作为个位上的数。若该两位数能被4整除，则甲胜，否则乙胜.
问：这个游戏公平吗？请说明理由。

查看试题解析
19.
如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6；若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？

查看试题解析

四、综合题

20. 如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．

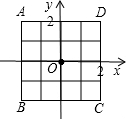(1)、求P点落在正方形ABCD面上（含正方形内部和边界）的概率．

(2)、将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD面上的概率为 $\frac{3}{4}$ ，若存在，指出其中的一种平移方式；若不存在，请说明理？

查看试题解析

21. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．如表是活动进行中的一组统计数据：

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	59	96	$b$	295	480	601
摸到白球的频率 $\frac{m}{n}$	$a$	0.64	0.58	0.59	0.60	0.601

(1)、请直接写出上表中的

a =

，

b =

；

(2)、请直接写出事件“摸到白球”的概率的估计值是（精确到

0.1

）；

(3)、如果袋中有12个白球，请你估计袋中除了白球外，还有多少个其它颜色的球？

查看试题解析

22. 从男女学生共36人的班级中，选一名班长，任何人都有同样的当选机会，如果选得男生的概率为 $\frac{2}{3}$ ．

(1)、求该班级男女生数各多少？

(2)、若该班转入女生6人，那么选得女生为班长的概率？

查看试题解析
23. 某校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、跳绳课，学生可以根据自己的爱好任选一项，老师根据学生报名情况进行了统计，并绘制了如图所示的尚未完成的频数分布直方图和扇形统计图，请你结合图中的信息，解答下列问题.

(1)、该校学生报名总人数有多少人？

(2)、从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？并补全两个统计图；

(3)、若从中随机抽一名学生，则该学生爱好跳绳的概率是多少？

查看试题解析

（人教版）2023-2024学年九年级数学上册 25.1 随机事件与概率 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册 25.1 随机事件与概率同步分层训练（培优卷）