(人教版)2023-2024学年九年级数学上册 24.4 弧长及扇形的面积 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
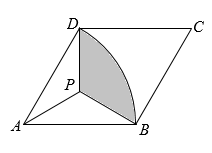 A、 B、 C、 D、
A、 B、 C、 D、 -
3. 如图,在中, , , , 点为的中点,以点为圆心作圆心角为的扇形 , 点恰在弧上,则图中阴影部分的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )
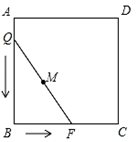 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )
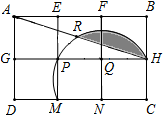 A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣2
A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣2 -
6. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
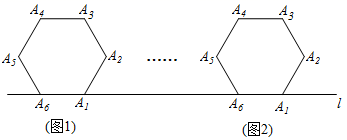 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 中国美食讲究色香味美,优雅的摆盘造型也会让美食錦上添花。图1中的摆盘,其形状是扇形的一部分,图2是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
 A、80π cm2 B、40π cm2 C、24π cm2 D、2π cm2
A、80π cm2 B、40π cm2 C、24π cm2 D、2π cm2 -
8. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
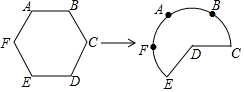 A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S2
A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S2 -
9. 如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF.AB=10,CD=6,EF=8,则图中阴影部分的面积等于( )
 A、10π B、12π C、 D、15π
A、10π B、12π C、 D、15π -
10. 如图,AB是⊙o直径,M,N是 上两点,C是 上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )
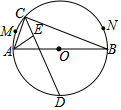 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径作弧(如图),则所得到的三条弧的长度之和为cm.(结果保留π)

-
12. 如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为 .

-
13. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为.

-
14. 如图,半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C,F,则图中阴影部分的面积为.
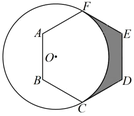
-
15. 如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为.

三、解答题
-
16. 如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
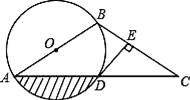 (1)、求证:DE是⊙O的切线;(2)、当DE=1,∠C=30°时,求图中阴影部分的面积.
(1)、求证:DE是⊙O的切线;(2)、当DE=1,∠C=30°时,求图中阴影部分的面积. -
17. 如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
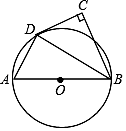 (1)、CD与⊙O有怎样的位置关系?请说明理由;(2)、若∠CDB=60°,AB=6,求 的长.
(1)、CD与⊙O有怎样的位置关系?请说明理由;(2)、若∠CDB=60°,AB=6,求 的长. -
18. 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
 (1)、求证:AD⊥CD;(2)、若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.)
(1)、求证:AD⊥CD;(2)、若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.) -
19.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1 .
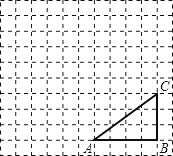 (1)、在正方形网格中,作出△AB1C1;(不要求写作法)
(1)、在正方形网格中,作出△AB1C1;(不要求写作法)
(2)、设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π).
四、综合题
-
20. 如图,是⊙O的直径,点A在⊙O上且平分弧 , 于点 , 分别交 , 于 , .
 (1)、求证:;(2)、若 , 求阴影部分面积.
(1)、求证:;(2)、若 , 求阴影部分面积. -
21. 如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。
 (1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,
(1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,①求证:HE=PE
②若BC=3,求点H运动轨迹的长度。
-
22. 如图,在矩形ABCD中,点E在边CB延长线上,AG⊥AE,交BC延长线于点G,边AG,DC交于点F,CF=BE,以AD为半径的⊙D交边BG于点P,Q,交AG于点M,延长DM交边QG于点N.
 (1)、求证:CG=AB.(2)、若AD=6,∠E=70°,求扇形ADM的面积.(3)、延长DC交⊙D于点H,且CH=NG,记AB=x,四边形AECF的面积为S,求S关于x的函数表达式.
(1)、求证:CG=AB.(2)、若AD=6,∠E=70°,求扇形ADM的面积.(3)、延长DC交⊙D于点H,且CH=NG,记AB=x,四边形AECF的面积为S,求S关于x的函数表达式. -
23. 如图,AB是⊙O的直径,点D,E在⊙O上,四边形BDEO是平行四边形,过点D作 交AE的延长线于点C.
 (1)、求证:CD是⊙O的切线.(2)、若 ,求阴影部分的面积.
(1)、求证:CD是⊙O的切线.(2)、若 ,求阴影部分的面积.
