(人教版)2023-2024学年九年级数学上册 24.4 弧长及扇形的面积 同步分层训练(基础卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 已知一个扇形的面积是 , 弧长是 , 则这个扇形的半径为( )A、24 B、22 C、12 D、62. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
 A、 B、 C、2π D、3. 若扇形的半径是弧长是 , 则扇形的面积为( )A、 B、 C、 D、4. 已知扇形的半径为6,圆心角为 , 则扇形的面积为( )A、 B、 C、 D、5. 如图,为了美化校园,学校在一块边角空地建造了一个扇形花圃,扇形圆心角∠AOB=120°,半径OA为3m,那么花圃的面积为( )
A、 B、 C、2π D、3. 若扇形的半径是弧长是 , 则扇形的面积为( )A、 B、 C、 D、4. 已知扇形的半径为6,圆心角为 , 则扇形的面积为( )A、 B、 C、 D、5. 如图,为了美化校园,学校在一块边角空地建造了一个扇形花圃,扇形圆心角∠AOB=120°,半径OA为3m,那么花圃的面积为( ) A、6πm2 B、3πm2 C、2πm2 D、πm26. 半径为6的圆弧的度数为 , 则它的弧长为( )A、 B、 C、 D、7. 若扇形的半径为3,圆心角为160°,则它的面积为( )A、2π B、3π C、4π D、9π8. 如图,已知的半径为 , 弦直径 , , 则的长为( )
A、6πm2 B、3πm2 C、2πm2 D、πm26. 半径为6的圆弧的度数为 , 则它的弧长为( )A、 B、 C、 D、7. 若扇形的半径为3,圆心角为160°,则它的面积为( )A、2π B、3π C、4π D、9π8. 如图,已知的半径为 , 弦直径 , , 则的长为( ) A、 B、 C、 D、9. 已知扇形的圆心角为120°,半径为3cm,则弧长为( )A、 B、2πcm C、4cm D、10. 已知,在圆中圆心角度数为45°,半径为10,则这个圆心角所对的扇形面积为( )A、 B、 C、 D、
A、 B、 C、 D、9. 已知扇形的圆心角为120°,半径为3cm,则弧长为( )A、 B、2πcm C、4cm D、10. 已知,在圆中圆心角度数为45°,半径为10,则这个圆心角所对的扇形面积为( )A、 B、 C、 D、二、填空题
-
11. 若一个扇形的半径为3,圆心角为120°,则此扇形的弧长为.12. 已知扇形所在的圆半径为6cm,面积为6πcm2 , 则扇形圆心角的度数为 .13. 扇形的半径为3,圆心角为90°,则该扇形的面积为.(结果保留)14. 如图,用一个半径为的定滑轮带动重物上升,滑轮上一点旋转了 , 假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了.
 15. 如图,已知⊙O的周长为4π,的长为π,则图中阴影部分的面积为.
15. 如图,已知⊙O的周长为4π,的长为π,则图中阴影部分的面积为.
三、解答题
-
16. 如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
 17. 如图,在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,求的度数.
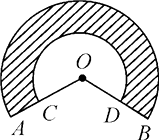
17. 如图,在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,求的度数. 18. 已知:如图,C,D是以为直径的半圆周的三等分点,.求阴影部分的面积?
18. 已知:如图,C,D是以为直径的半圆周的三等分点,.求阴影部分的面积? 19. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
19. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
四、综合题
-
20. 如图,点、、都在上,过点作交延长线于点 , 连接、 , 且 , cm.
 (1)、求证:是的切线;(2)、求的半径长;(3)、求由弦、与弧所围成的阴影部分的面积.
(1)、求证:是的切线;(2)、求的半径长;(3)、求由弦、与弧所围成的阴影部分的面积.


