(人教版)2023-2024学年九年级数学上册 24.3 正多边形和圆 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).
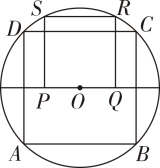 A、1 :2 B、1:3 C、2:3 D、2:52. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法不正确的是( )
A、1 :2 B、1:3 C、2:3 D、2:52. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法不正确的是( )
甲
乙是的垂直平分线
丙是等腰三角形
丁与平行
A、甲 B、乙 C、丙 D、丁3. 如图,点O为正六边形的中心,P,Q分别从点同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第次相遇地点的坐标为( ) A、 B、 C、 D、4. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )
A、 B、 C、 D、4. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )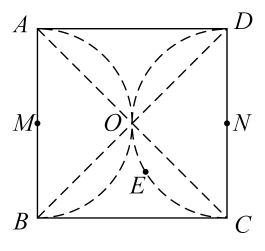 A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得5. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )
A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得5. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )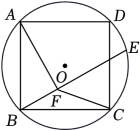 A、 B、1 C、 D、6. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )
A、 B、1 C、 D、6. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( ) A、1 B、2 C、3 D、47. 已知矩形MNPQ的顶点M,N,P,Q分别在正六边形ABCDEF的边DE,FA,AB,CD上,且 . 在点从移向(与不重合)的过程中,下列的判断中,正确的是( )
A、1 B、2 C、3 D、47. 已知矩形MNPQ的顶点M,N,P,Q分别在正六边形ABCDEF的边DE,FA,AB,CD上,且 . 在点从移向(与不重合)的过程中,下列的判断中,正确的是( )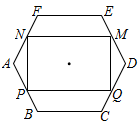 A、矩形MNPQ的面积与周长保持不变 B、矩形MNPQ的面积逐渐减小,周长逐渐增大 C、矩形MNPQ的面积与周长均逐渐增大 D、矩形MNPQ的面积与周长均逐渐减小8. 如图,正六边形 中,点 是边 上的点,记图中各三角形的面积依次为 ,则下列判断正确的是( )
A、矩形MNPQ的面积与周长保持不变 B、矩形MNPQ的面积逐渐减小,周长逐渐增大 C、矩形MNPQ的面积与周长均逐渐增大 D、矩形MNPQ的面积与周长均逐渐减小8. 如图,正六边形 中,点 是边 上的点,记图中各三角形的面积依次为 ,则下列判断正确的是( ) A、 B、 C、 D、9. 如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若 , 则表示实数a的点落在数轴上(如图2)标有四段中的( )
A、 B、 C、 D、9. 如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若 , 则表示实数a的点落在数轴上(如图2)标有四段中的( )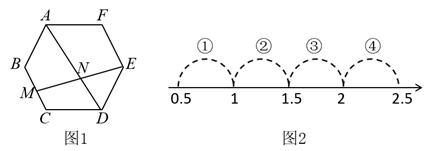 A、段① B、段② C、段③ D、段④10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、段① B、段② C、段③ D、段④10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )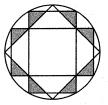 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 如图,已知点M在正六边形的边上运动,如果 , 那么线段的长度的取值范围是 .
 12. 已知中, , 含角的三个顶点分在的三边上,且直角顶点D在斜边上,则的长为 .13. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有 .
12. 已知中, , 含角的三个顶点分在的三边上,且直角顶点D在斜边上,则的长为 .13. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有 .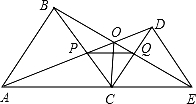 14. 如图,在⊙O中,∠CBO=55°,CAO=15°,则∠AOB的度数是.
14. 如图,在⊙O中,∠CBO=55°,CAO=15°,则∠AOB的度数是. 15. 如图,边长为6的正方形内接于 , 点E是上的一动点(不与A , B重合,点F是上的一点,连接 , 分别与交于点G , H , 且 , 有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是.(填序号)
15. 如图,边长为6的正方形内接于 , 点E是上的一动点(不与A , B重合,点F是上的一点,连接 , 分别与交于点G , H , 且 , 有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是.(填序号)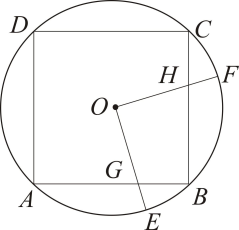
三、解答题
-
16. 如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连结AP.求AP的长.
 17. 如图,四边形ABCD内接于⊙O,∠BAD=90°, = ,过点C作CE⊥AD,垂足为E,若AE=3,DE= ,求∠ABC的度数.
17. 如图,四边形ABCD内接于⊙O,∠BAD=90°, = ,过点C作CE⊥AD,垂足为E,若AE=3,DE= ,求∠ABC的度数.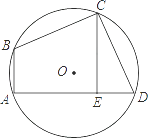 18. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
18. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).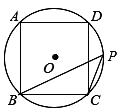 (1)、求∠BPC的度数;
(1)、求∠BPC的度数;
(2)、若⊙O的半径为8,求正方形ABCD的边长.19. 如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P.若∠P=30°,∠ABC=100°,求∠C的度数.
四、综合题
-
20. 如图,在等边三角形中,为上的一点,过点做的平行线交于点 , 点是线段上的动点(点不与重合).将绕点逆时针方向旋转 , 得到 , 连接交于 .
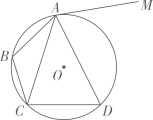
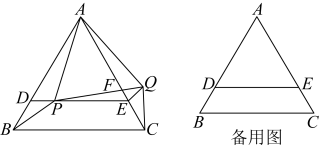 (1)、证明:在点的运动过程中,总有 .(2)、当为何值时,是直角三角形?21. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .
(1)、证明:在点的运动过程中,总有 .(2)、当为何值时,是直角三角形?21. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .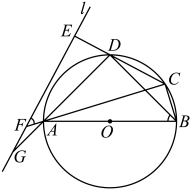 (1)、求证:直线直线;(2)、若;
(1)、求证:直线直线;(2)、若;①求证:;
②若 , 求四边形的周长.