(人教版)2023-2024学年九年级数学上册 24.3 正多边形和圆 同步分层训练(提升卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、22. 已知点O是△ABC的外心,∠BOC= 80°,则∠BAC的度数为( ).A、40° B、100° C、40°或140° D、40或100°3. 已知四边形ABCD内接于圆,则∠A,∠B,∠C,∠D的度数比可能是( ).A、1:2:3:4 B、7:5:10:8 C、13:1 :5:17 D、1:3:2:44. 若正多边形的一个内角是144°,则该正多边形的边数是( )A、8 B、9 C、10 D、115. 一元钱硬币的直径约为24mm,则用它能完全覆盖住的正六边形的边长最大不超过( ).A、12 mm B、 mm C、6mm D、mm6. 如图,△ABC内接于⊙O,D,E为圆上的点,连结AD,BD,AE,CE.若∠BAC=50°,则∠D与∠E的和为( )
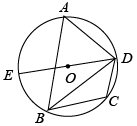
 A、220° B、230° C、240° D、250°7. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠A=50°,则∠BCE的度数为( ).
A、220° B、230° C、240° D、250°7. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠A=50°,则∠BCE的度数为( ).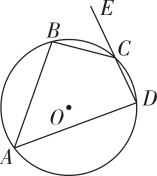 A、40° B、50° C、60° D、130°8. 如图,∠ AOB=100°.点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ).
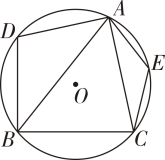
A、40° B、50° C、60° D、130°8. 如图,∠ AOB=100°.点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ). A、50° B、80°或 50° C、130° D、50°或130°9. 如图所示,四边形ABCD内接于 , 若 , 则的度数是( ).
A、50° B、80°或 50° C、130° D、50°或130°9. 如图所示,四边形ABCD内接于 , 若 , 则的度数是( ).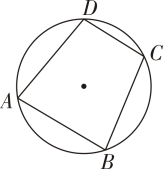 A、 B、 C、 D、10. 如图所示,四边形是的内接四边形, , , 则AD的长为( ).
A、 B、 C、 D、10. 如图所示,四边形是的内接四边形, , , 则AD的长为( ).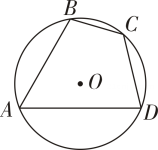 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
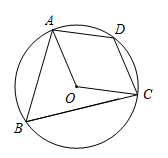
11. 如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的大小为
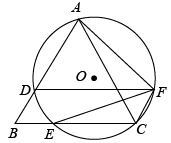
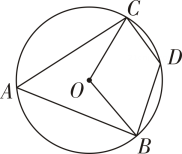 12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是
12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是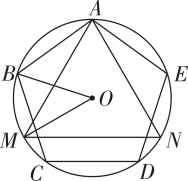 13. 边长相等的正五边形和正六边形如图所示拼接在一起,则∠ABC的度数是
13. 边长相等的正五边形和正六边形如图所示拼接在一起,则∠ABC的度数是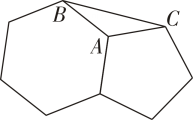 14. 如图,AB 是⊙O的直径,C,D是上两点.若∠ADC=120°,则∠BAC的度数是
14. 如图,AB 是⊙O的直径,C,D是上两点.若∠ADC=120°,则∠BAC的度数是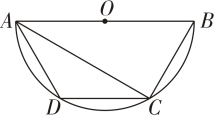 15. 在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是
15. 在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是三、解答题
-
16. 如图,以正六边形ABCDEF的边AB为边,在正六边形内作正方形ABMN,连结MC.求∠BCM的度数.
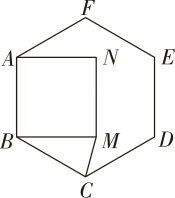 17. 如图,O是正八边形的外接圆的圆心,M,N分别是正八边形相邻的边AB,BC上的点,且AM=BN.求∠MON的度数.
17. 如图,O是正八边形的外接圆的圆心,M,N分别是正八边形相邻的边AB,BC上的点,且AM=BN.求∠MON的度数.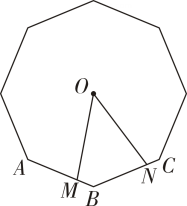 18. 如图,在正十二边形A1A2……A12 中,连结A3A7 , A7A10 , 求∠A3A7A10的度数.
18. 如图,在正十二边形A1A2……A12 中,连结A3A7 , A7A10 , 求∠A3A7A10的度数.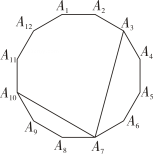 19. 已知:如图,四边形ABCD内接于⊙O,且AD是⊙O的直径,C是的中点,AB与DC的延长线交于⊙O外一点E.求证:BC= EC.
19. 已知:如图,四边形ABCD内接于⊙O,且AD是⊙O的直径,C是的中点,AB与DC的延长线交于⊙O外一点E.求证:BC= EC.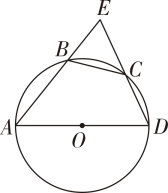
四、综合题