(人教版)2023-2024学年九年级数学上册 24.3 正多边形和圆 同步分层训练(基础卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ).
 A、45° B、50° C、60° D、75°2. 如图,延长圆内接四边形ABCD的边AB,DC,相交于点E,延长边AD,BC,相交于点F.若∠E=30°,∠F=50° ,则∠A的度数为( ).
A、45° B、50° C、60° D、75°2. 如图,延长圆内接四边形ABCD的边AB,DC,相交于点E,延长边AD,BC,相交于点F.若∠E=30°,∠F=50° ,则∠A的度数为( ). A、20° B、30° C、50° D、60°3. 如图所示,四边形ABCD内接于.已知 , 则的大小是( ).
A、20° B、30° C、50° D、60°3. 如图所示,四边形ABCD内接于.已知 , 则的大小是( ). A、 B、 C、 D、4. 若一个多边形的每一个外角都是40°,则这个多边形的边数是( )A、7 B、8 C、9 D、105. 正十边形的一个外角的度数为( )A、144° B、120° C、60° D、36°6. 若一个正n边形的每个外角为30°,则这个正n边形的边数是( )A、10 B、11 C、12 D、147. 如图,在中,点A、B、C在圆上,点D在AB的延长线上,已知 , 则( )
A、 B、 C、 D、4. 若一个多边形的每一个外角都是40°,则这个多边形的边数是( )A、7 B、8 C、9 D、105. 正十边形的一个外角的度数为( )A、144° B、120° C、60° D、36°6. 若一个正n边形的每个外角为30°,则这个正n边形的边数是( )A、10 B、11 C、12 D、147. 如图,在中,点A、B、C在圆上,点D在AB的延长线上,已知 , 则( )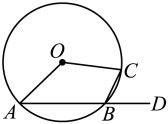 A、 B、 C、 D、8. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A、 B、 C、 D、8. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )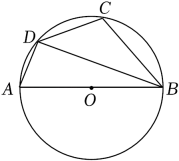 A、90° B、100° C、110° D、120°9. 如图,四边形ABCD是⊙O的内接四边形,E是BC延长线上一点.若∠BAD=114°,则∠DCE的度数是( )
A、90° B、100° C、110° D、120°9. 如图,四边形ABCD是⊙O的内接四边形,E是BC延长线上一点.若∠BAD=114°,则∠DCE的度数是( )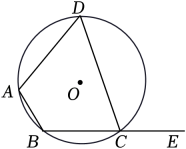 A、124° B、114° C、94° D、66°10. 如图,四边形是的内接四边形,若 , 则的度数为( )
A、124° B、114° C、94° D、66°10. 如图,四边形是的内接四边形,若 , 则的度数为( )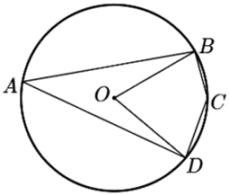 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
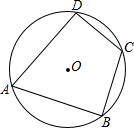
11. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是.
 12. 若正多边形的一个外角为45°,则此正多边形为正边形.13. 一个边长为2的正六边形,其外接圆的半径为.14. 已知四边形内接于 , 若 , 则的度数为.15. 如图,四边形的四个顶点均在半圆上,若 , 则.
12. 若正多边形的一个外角为45°,则此正多边形为正边形.13. 一个边长为2的正六边形,其外接圆的半径为.14. 已知四边形内接于 , 若 , 则的度数为.15. 如图,四边形的四个顶点均在半圆上,若 , 则.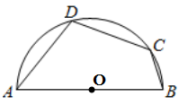
三、解答题
-
16. 如图所示,在⊙O的内接四边形ABCD中,AB=AD,∠C=100°.若点E在上,求∠E的度数.
 17. 已知在△ABC中,AB=AC , 以AB为直径的⊙O分别交AC于点 D , BC于点E , 连接ED . 求证:ED=EC .
17. 已知在△ABC中,AB=AC , 以AB为直径的⊙O分别交AC于点 D , BC于点E , 连接ED . 求证:ED=EC .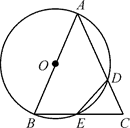 18. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,求∠BCD的度数.
18. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,求∠BCD的度数.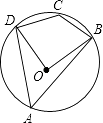 19. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.
19. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.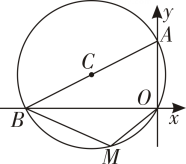
四、综合题
-
20. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.
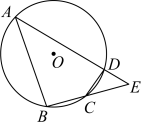 (1)、求证:.(2)、若 , 点为的中点,求的半径.
(1)、求证:.(2)、若 , 点为的中点,求的半径.