(人教版)2023-2024学年九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( )
 A、 B、 C、- D、-22. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A、 B、 C、- D、-22. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )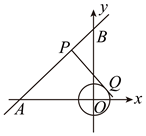 A、 B、2.4 C、 D、33. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( )
A、 B、2.4 C、 D、33. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( ) A、4 B、8 C、10 D、64. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )
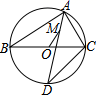
A、4 B、8 C、10 D、64. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )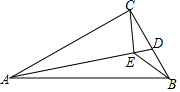 A、1 B、 C、2 D、5. 如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )
A、1 B、 C、2 D、5. 如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )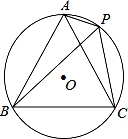 A、当弦PB最长时,△APC是等腰三角形 B、当△APC是等腰三角形时,PO⊥AC C、当PO⊥AC时,∠ACP=30° D、当∠ACP=30°时,△BPC是直角三角形6. 图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A、当弦PB最长时,△APC是等腰三角形 B、当△APC是等腰三角形时,PO⊥AC C、当PO⊥AC时,∠ACP=30° D、当∠ACP=30°时,△BPC是直角三角形6. 图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( ) A、3 B、4 C、5 D、3.57. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( )
A、3 B、4 C、5 D、3.57. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( ) A、72 B、96 C、120 D、1449. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且☉O的半径长为1,则下列结论不成立的是( )
A、72 B、96 C、120 D、1449. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且☉O的半径长为1,则下列结论不成立的是( )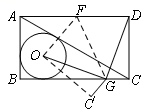 A、CD+DF=4 B、CD−DF=2 −3 C、BC+AB=2 +4 D、BC−AB=210. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为( )
A、CD+DF=4 B、CD−DF=2 −3 C、BC+AB=2 +4 D、BC−AB=210. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为( )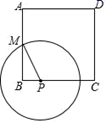 A、3或 B、3或 C、5或 D、5或
A、3或 B、3或 C、5或 D、5或二、填空题
-
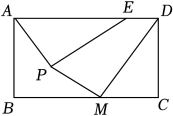
11. 在矩形 中, , 点E在边上, , 点P为矩形内一点且 , 点M为边上一点,连接 , 则的最小值为 .
 12. 如图,和都是等边三角形, , , 固定 , 把绕点C旋转任意角度,连接AD,BE,设AD,BE所在的直线交于点O,则在旋转过程中,始终有 , 且的大小保持不变,这时点O到直线AB的最大距离为 .
12. 如图,和都是等边三角形, , , 固定 , 把绕点C旋转任意角度,连接AD,BE,设AD,BE所在的直线交于点O,则在旋转过程中,始终有 , 且的大小保持不变,这时点O到直线AB的最大距离为 .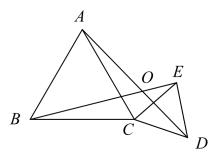 13. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是 .
13. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是 . 14. 如图,已知等边△ABC内接于⊙O,点P为上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为 . (用含α的代数式表示)
14. 如图,已知等边△ABC内接于⊙O,点P为上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为 . (用含α的代数式表示)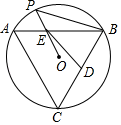 15. 如图,在△ABC中,AC=3,BC=4 ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为.
15. 如图,在△ABC中,AC=3,BC=4 ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为.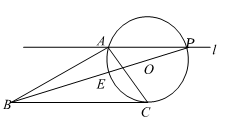
三、解答题
-
16. 如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
 (1)、求证:AP=AB;(2)、若OB=4,AB=3,求线段BP的长.17. 如图,已知△ABC,∠B=40°.
(1)、求证:AP=AB;(2)、若OB=4,AB=3,求线段BP的长.17. 如图,已知△ABC,∠B=40°. (1)、在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);(2)、连接EF,DF,求∠EFD的度数.18. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)、在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);(2)、连接EF,DF,求∠EFD的度数.18. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.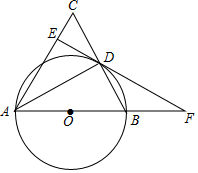 (1)、求证:DE与⊙O相切;(2)、若CD=BF,AE=3,求DF的长.19. 如图,AB为⊙O直径,C为⊙O上一点,点D是 的中点,DE⊥AC于E,DF⊥AB于F.
(1)、求证:DE与⊙O相切;(2)、若CD=BF,AE=3,求DF的长.19. 如图,AB为⊙O直径,C为⊙O上一点,点D是 的中点,DE⊥AC于E,DF⊥AB于F.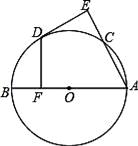 (1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.
(1)、判断DE与⊙O的位置关系,并证明你的结论;(2)、若OF=4,求AC的长度.四、综合题
-
20. 如图1,是的直径,过点B作的切线 , 弦 , 交于点F,且 , 连接、 , 延长交于点E.
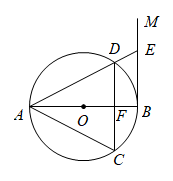 (1)、求证:是等边三角形;(2)、连接 , 若 , 求的长.21. 如图,在△ABC中,D在边AC上,圆O为锐角△BCD的外接圆,连结CO并延长交AB于点E.
(1)、求证:是等边三角形;(2)、连接 , 若 , 求的长.21. 如图,在△ABC中,D在边AC上,圆O为锐角△BCD的外接圆,连结CO并延长交AB于点E. (1)、若∠DBC=α,请用含α的代数式表示∠DCE;(2)、如图2,作BF⊥AC,垂足为F,BF与CE交于点G,已知∠ABD=∠CBF.
(1)、若∠DBC=α,请用含α的代数式表示∠DCE;(2)、如图2,作BF⊥AC,垂足为F,BF与CE交于点G,已知∠ABD=∠CBF.①求证:EB=EG;
②若CE=5,AC=8,求FG+FB的值.