(人教版)2023-2024学年九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步分层训练(提升卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点).以A为圆心,r为半径作图.选取的格点中,若除A外恰好有3个在圆内,则r的取值范围为( ).
 A、<r< B、<r< C、<r<5 D、5<r<2. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、43. 已知⊙O的半径为3cm,P为圆外一点,则OP的长可能是( ).A、1cm B、2cm C、3cm D、4cm4. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D.则∠C=( )
A、<r< B、<r< C、<r<5 D、5<r<2. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、43. 已知⊙O的半径为3cm,P为圆外一点,则OP的长可能是( ).A、1cm B、2cm C、3cm D、4cm4. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D.则∠C=( ) A、30° B、40° C、45° D、60°5. 如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( )
A、30° B、40° C、45° D、60°5. 如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( ) A、68° B、64° C、58° D、56°6. 如图,点P为外一点,连结 , 作以为直径的圆,两圆交于点Q,连接 , 可得是的切线,则判定其为切线的依据是( )
A、68° B、64° C、58° D、56°6. 如图,点P为外一点,连结 , 作以为直径的圆,两圆交于点Q,连接 , 可得是的切线,则判定其为切线的依据是( ) A、经过半径的外端并且垂直这条半径的直线是圆的切线 B、垂线段最短 C、过直线外一点,有且只有一条直线与已知直线垂直 D、过圆外一点所作的圆的两条切线长相等7. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、8. 如图,抛物线与x轴交于A、B两点,抛物线的顶点为D,点C为的中点,以C为圆心,长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接 , 取的中点F,当点E沿着半圆从点A运动至点B的过程中,线段 的最小值为( )
A、经过半径的外端并且垂直这条半径的直线是圆的切线 B、垂线段最短 C、过直线外一点,有且只有一条直线与已知直线垂直 D、过圆外一点所作的圆的两条切线长相等7. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、8. 如图,抛物线与x轴交于A、B两点,抛物线的顶点为D,点C为的中点,以C为圆心,长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接 , 取的中点F,当点E沿着半圆从点A运动至点B的过程中,线段 的最小值为( )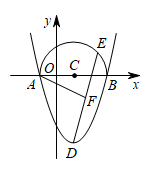 A、 B、 C、 D、9. 已知直角三角形两条直角边为3,4,则它的外接圆半径为( )A、1.5 B、2 C、2.5 D、510. 已知的半径为 , 点P到圆心O的距离为 , 则点( )A、在圆内 B、在圆上 C、在圆外 D、在圆上或圆外
A、 B、 C、 D、9. 已知直角三角形两条直角边为3,4,则它的外接圆半径为( )A、1.5 B、2 C、2.5 D、510. 已知的半径为 , 点P到圆心O的距离为 , 则点( )A、在圆内 B、在圆上 C、在圆外 D、在圆上或圆外二、填空题
-
11. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是
 12. 如图,量角器的零度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为120°,则该直尺的宽度为cm.
12. 如图,量角器的零度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为120°,则该直尺的宽度为cm. 13. 一个点到圆上最近点的距离为4,最远点的距离为8,则此圆的直径是.14. 如图所示,在矩形ABCD中,AB=4,AD=3,以点D为圆心作半径为x的圆,使A,B,C三点都在圆外,则x的取值范围是.
13. 一个点到圆上最近点的距离为4,最远点的距离为8,则此圆的直径是.14. 如图所示,在矩形ABCD中,AB=4,AD=3,以点D为圆心作半径为x的圆,使A,B,C三点都在圆外,则x的取值范围是. 15. 一个点到圆上的点的最小距离为6cm , 最大距离为10cm , 则圆的半径为cm .
15. 一个点到圆上的点的最小距离为6cm , 最大距离为10cm , 则圆的半径为cm .三、解答题
-
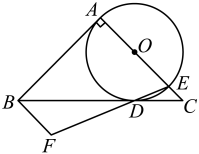
16. 如图所示,在中,是的平分线上一点,于点 , 过点作交AB于点.求证:点是A,B,D三点的外接圆的圆心.
 17. 如图,直线经过上的点A , 且 , . 求证:直线是的切线.
17. 如图,直线经过上的点A , 且 , . 求证:直线是的切线. 18. 如图,圆是的内切圆,其中 , , 求其内切圆的半径.
18. 如图,圆是的内切圆,其中 , , 求其内切圆的半径. 19. 如图,某海域以点A为圆心、为半径的圆形区域为多暗礁的危险区,但渔业资源丰富,渔船要从点B处前往A处进行捕鱼,B、A两点之间的距离是 , 如果渔船始终保持的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?
19. 如图,某海域以点A为圆心、为半径的圆形区域为多暗礁的危险区,但渔业资源丰富,渔船要从点B处前往A处进行捕鱼,B、A两点之间的距离是 , 如果渔船始终保持的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?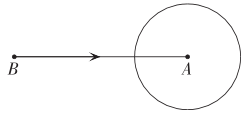
四、综合题
-
20. 如图,是的直径,点在上.过点作的切线 , 过点作于点 .
 (1)、求证:平分;(2)、连接 , 若 , , 求的长.
(1)、求证:平分;(2)、连接 , 若 , , 求的长.