(人教版)2023-2024学年九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步分层训练(基础卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等2. 已知⊙O的半径是6,点A到圆心O的距离是5,则点A与⊙O的位置关系是( ).A、点A在⊙O上 B、点A在⊙O内 C、点A在⊙O外 D、点A与圆心O重合3. 小张不慎把家里的圆形玻璃打碎了,其中4块碎片如图所示,为了配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( ).
 A、① B、② C、③ D、④4. 三角形的外心在( ).A、三角形内 B、三角形外 C、三角形一边上 D、三角形三边中垂线的交点5. 若的半径为5,点到圆心的距离为 , 当点在圆上时,则有( ).A、 B、 C、 D、6. 在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )A、点A在⊙C内 B、点A在⊙C上 C、点A在⊙C外 D、无法确定7. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定8. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
A、① B、② C、③ D、④4. 三角形的外心在( ).A、三角形内 B、三角形外 C、三角形一边上 D、三角形三边中垂线的交点5. 若的半径为5,点到圆心的距离为 , 当点在圆上时,则有( ).A、 B、 C、 D、6. 在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )A、点A在⊙C内 B、点A在⊙C上 C、点A在⊙C外 D、无法确定7. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定8. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )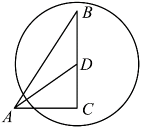 A、 B、 C、 D、9. 已知圆的半径为5cm,同一平面内一点到圆心的距离是6cm,则这点在( )A、圆外 B、圆上 C、圆内 D、不能确定10. 如图,是的直径,点D在的延长线上,切于点C,若 , 则等于( )
A、 B、 C、 D、9. 已知圆的半径为5cm,同一平面内一点到圆心的距离是6cm,则这点在( )A、圆外 B、圆上 C、圆内 D、不能确定10. 如图,是的直径,点D在的延长线上,切于点C,若 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示,正方形网格中的每个小正方形的边长都相等,的三个顶点A,B,C都在格点上,若不与顶点重合的格点D在的外接圆上,则图中符合条件的点D有个.
 12. 平面上有及一点 , 点到上一点的距离最长为 , 最短为 , 则的半径为.13. 的半径是 , 点P与圆心O的距离是 , 则点在.(填写“内”、“上”、“外”)14. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.
12. 平面上有及一点 , 点到上一点的距离最长为 , 最短为 , 则的半径为.13. 的半径是 , 点P与圆心O的距离是 , 则点在.(填写“内”、“上”、“外”)14. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.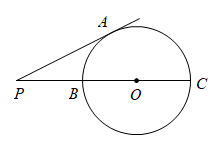 15. 在中, , 则外接圆半径R=.
15. 在中, , 则外接圆半径R=.三、解答题
-
16. 如图所示,在一个长度为8的梯子AB的顶点向点滑动的过程中,梯子的两端A,B与墙的底端构成的三角形的外心与点的距离是否发生变化?若发生变化,请说明理由;若不发生变化,请求出其长度.
 17. 如图,D为⊙O上一点,点C在直径BA的延长线上,且 .求证:CD是⊙O的切线.
17. 如图,D为⊙O上一点,点C在直径BA的延长线上,且 .求证:CD是⊙O的切线. 18. 如图,AB与⊙O相切于点B,AO及AO的延长线分别交⊙O于D、C两点,若∠A=40°,求∠C的度数.
18. 如图,AB与⊙O相切于点B,AO及AO的延长线分别交⊙O于D、C两点,若∠A=40°,求∠C的度数.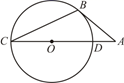 19. 如图,CD是⊙O的直径,并且AC=BC,AD=BD.求证:直线AB是⊙O的切线.
19. 如图,CD是⊙O的直径,并且AC=BC,AD=BD.求证:直线AB是⊙O的切线.
四、综合题
-
20. 如图,点A、B、C在上, , 直线 , , 点O在上.
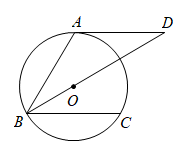 (1)、判断直线与的位置关系,并说明理由;(2)、若的半径为4,求弦的长.
(1)、判断直线与的位置关系,并说明理由;(2)、若的半径为4,求弦的长.