(人教版)2023-2024学年九年级数学上册 24.1 圆的有关性质 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )
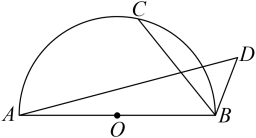 A、2+2 B、+1 C、3 D、2+12. 如图,已知点均在上,为的直径,弦的延长线与弦的延长线交于点 , 连接 . 则下列命题为假命题的是( )
A、2+2 B、+1 C、3 D、2+12. 如图,已知点均在上,为的直径,弦的延长线与弦的延长线交于点 , 连接 . 则下列命题为假命题的是( )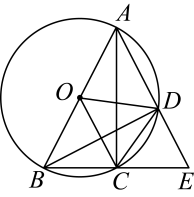 A、若点是的中点,则 B、若 , 则 C、若 , 则 D、若半径平分弦 , 则四边形是平行四边形3. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( )
A、若点是的中点,则 B、若 , 则 C、若 , 则 D、若半径平分弦 , 则四边形是平行四边形3. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( ) A、5 B、18 C、3 D、174. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )
A、5 B、18 C、3 D、174. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( ) A、1 B、2 C、3 D、45. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )
A、1 B、2 C、3 D、45. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )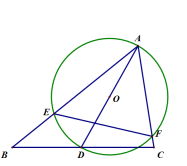 A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小6. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小6. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:①AD2+AC2=4;②∠DBC+∠ADO=90°;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
其中正确的是( )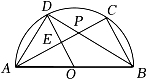 A、①②③ B、②③④ C、③④ D、②④7. 如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且= , 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON= , 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
A、①②③ B、②③④ C、③④ D、②④7. 如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且= , 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON= , 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )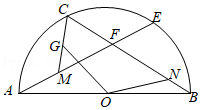 A、先变大后变小 B、先变小后变大 C、保持不变 D、一直减小8. 如图,E为正方形ABCD的边CD上一动点,AB=2,连接BE,过A作AF⊥BE,交BC于F,交BE于G,连接CG,当CG为最小值时,CF的长为( )
A、先变大后变小 B、先变小后变大 C、保持不变 D、一直减小8. 如图,E为正方形ABCD的边CD上一动点,AB=2,连接BE,过A作AF⊥BE,交BC于F,交BE于G,连接CG,当CG为最小值时,CF的长为( ) A、 B、 C、 D、9. 如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )
A、 B、 C、 D、9. 如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )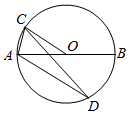 A、3 B、 C、 D、10. 如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
A、3 B、 C、 D、10. 如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )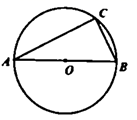 A、0个 B、2个 C、3个 D、4个
A、0个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,AB,CD是⊙O的两条直径,∠AOC=50°.过点A作AE∥CD,交⊙O于点E,则的度数为
 12. 如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为.
12. 如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为. 13. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.
13. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.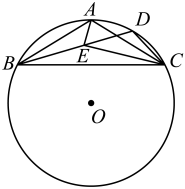 14. 如图,正方形的边长为4,点分别在上,且 , 过三点作交于点G.在点F整个运动过程中,当中满足某两条线段相等时,的长为.
14. 如图,正方形的边长为4,点分别在上,且 , 过三点作交于点G.在点F整个运动过程中,当中满足某两条线段相等时,的长为. 15. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
15. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=60°;②∠CED= ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是 .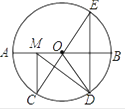
三、解答题
-
16. 如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
 (1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.17. 如图,A 是⊙O上的一个六等分点,B是的中点,P是直径MN上的一个动点,⊙O的半径为1.
(1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.17. 如图,A 是⊙O上的一个六等分点,B是的中点,P是直径MN上的一个动点,⊙O的半径为1. (1)、 找出当AP+BP取最小值时,点P的位置.(2)、求AP+BP的最小值.18. 研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图甲所示,已知四边形ABCD内接于 , 对角线 , 且AC⊥BD.
(1)、 找出当AP+BP取最小值时,点P的位置.(2)、求AP+BP的最小值.18. 研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图甲所示,已知四边形ABCD内接于 , 对角线 , 且AC⊥BD.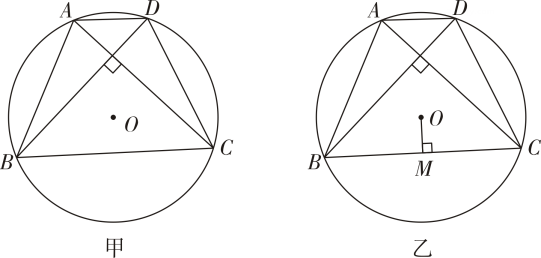 (1)、求证:AB=CD.(2)、若的半径为8,的度数为120°,求四边形ABCD的面积.(3)、如图乙所示,作OM⊥BC于点M,请猜测OM与AD的数量关系并证明.19. 如图所示,在中,直径 , 弦 , 直线AD,BC相交于点.
(1)、求证:AB=CD.(2)、若的半径为8,的度数为120°,求四边形ABCD的面积.(3)、如图乙所示,作OM⊥BC于点M,请猜测OM与AD的数量关系并证明.19. 如图所示,在中,直径 , 弦 , 直线AD,BC相交于点.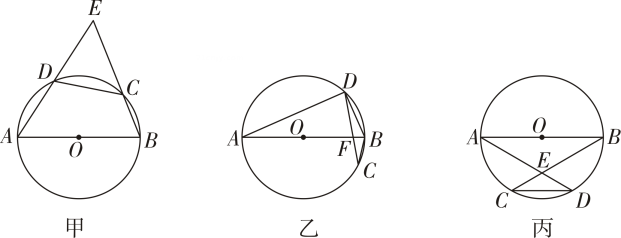 (1)、如图甲所示,的度数为.(2)、如图乙所示,AB与CD交于点 , 请补全图形并求的度数.(3)、如图丙所示,直径AB与弦CD不相交,求的度数.
(1)、如图甲所示,的度数为.(2)、如图乙所示,AB与CD交于点 , 请补全图形并求的度数.(3)、如图丙所示,直径AB与弦CD不相交,求的度数.四、综合题
-
20. 已知,是直径,弦于点 , 点是上一点.
 (1)、如图1,连接、、 , 求证:平分;(2)、如图2,连接、、 , 交于点 , 交于点 , 若;求证:;(3)、如图 , 在(2)的条件下,连接交于 , 连接 , 若 , , 求半径.21. 已知钝角三角形内接于分别为的中点,连接.
(1)、如图1,连接、、 , 求证:平分;(2)、如图2,连接、、 , 交于点 , 交于点 , 若;求证:;(3)、如图 , 在(2)的条件下,连接交于 , 连接 , 若 , , 求半径.21. 已知钝角三角形内接于分别为的中点,连接. (1)、如图1,当点在同一条直线上时,求证:.(2)、如图2,当不在同一条直线上时,取的中点 , 连接交于点 , 当时.
(1)、如图1,当点在同一条直线上时,求证:.(2)、如图2,当不在同一条直线上时,取的中点 , 连接交于点 , 当时.①求证:是等腰三角形;
②如图3,连并延长交于点 , 连接.求证:.
22. 已知内接于 , 的平分线交于点 , 连接 , . (1)、如图①,当时,请直接写出线段 , , 之间满足的等量关系式:;(2)、如图②,当时,试探究线段 , , 之间满足的等量关系,并证明你的结论.23. 数学活动课上,老师给出这样一个题目:如图1,点C是弧上的点,于D,于E,若 , 求证:点C是弧的中点.
(1)、如图①,当时,请直接写出线段 , , 之间满足的等量关系式:;(2)、如图②,当时,试探究线段 , , 之间满足的等量关系,并证明你的结论.23. 数学活动课上,老师给出这样一个题目:如图1,点C是弧上的点,于D,于E,若 , 求证:点C是弧的中点.小波同学想到的办法是:可通过证明来完成它.
 (1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.
(1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.如图2,已知是的直径,点D,点E分别是半径 , 的中点,延长交于点F,若于D,且点C是弧的中点,求证: , 请你证明.
(3)、拓展:如图3,在(2)的条件下,点G是弧上一点,连接 , , 若 , , 求的半径长.