(人教版)2023-2024学年九年级数学上册 24.1 圆的有关性质 同步分层训练(提升卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,是的弦,半径 , 为圆周上一点,若所对应圆心角的度数为 , 则的度数为( )
 A、 B、 C、 D、2. 如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时位于弧AB上,此时∠AOE=56°,则α的度数是( ).
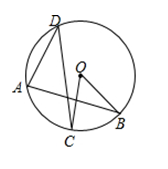
A、 B、 C、 D、2. 如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时位于弧AB上,此时∠AOE=56°,则α的度数是( ).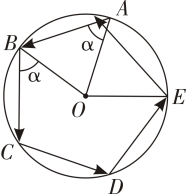 A、52° B、60° C、72° D、76°3. 如图,BC是半圆O的直径,D,E是上两点,连结BD,CE并延长,交于点A,连结OD,OE.若∠A=70° ,则∠DOE的度数为( ).
A、52° B、60° C、72° D、76°3. 如图,BC是半圆O的直径,D,E是上两点,连结BD,CE并延长,交于点A,连结OD,OE.若∠A=70° ,则∠DOE的度数为( ). A、35° B、38° C、40° D、42°4. 数学课上,老师让学生用尺规作图作Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法能判断∠ACB是直角的依据是( ).
A、35° B、38° C、40° D、42°4. 数学课上,老师让学生用尺规作图作Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法能判断∠ACB是直角的依据是( ). A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径5. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连结OA,OB,BC.若∠ABC= 20°,则∠AOB的度数是( ).
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径5. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连结OA,OB,BC.若∠ABC= 20°,则∠AOB的度数是( ). A、40° B、50° C、70° D、80°6. 已知∠ADB,作图:
A、40° B、50° C、70° D、80°6. 已知∠ADB,作图:
步骤1:以点D为圆心,适当长为半径作弧,分别交DA,DB于点M,N;再分别以点M,N为圆心,大于MN长为半径作弧,交于点E ,作射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径作半圆,分别交DA,DB,DE于点P,Q,C.
步骤3:连结PQ,OC.
有下列判断:
①= ;②OC∥DA ;③DP= PQ;④OC垂直平分PQ.
其中正确的有( ).
A、①③④ B、①②④ C、②③④ D、①②③④7. 如图,BC是⊙O的直径,A是⊙O上的一点.若∠OAC=32°,则∠B的度数是( ). A、58° B、60° C、64° D、68°8. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上一点.若∠BOC=40° ,则∠D的度数为( ).
A、58° B、60° C、64° D、68°8. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上一点.若∠BOC=40° ,则∠D的度数为( ). A、100° B、110° C、120° D、130°9. 已知点O是△ABC的外心,∠BOC= 80°,则∠BAC的度数为( ).A、40° B、100° C、40°或140° D、40或100°10. 已知四边形ABCD内接于圆,则∠A,∠B,∠C,∠D的度数比可能是( ).A、1:2:3:4 B、7:5:10:8 C、13:1 :5:17 D、1:3:2:4
A、100° B、110° C、120° D、130°9. 已知点O是△ABC的外心,∠BOC= 80°,则∠BAC的度数为( ).A、40° B、100° C、40°或140° D、40或100°10. 已知四边形ABCD内接于圆,则∠A,∠B,∠C,∠D的度数比可能是( ).A、1:2:3:4 B、7:5:10:8 C、13:1 :5:17 D、1:3:2:4二、填空题
-
11. 如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的大小为
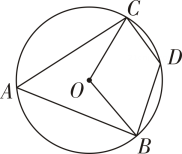 12. 如图,EF是⊙O的直径,把∠A为45°的直角三角尺ABC的一条直角边BC放在直线EF上,斜边AB所在直线与⊙O交于点P,点B,O重合,且AC大于OE.将三角尺ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是
12. 如图,EF是⊙O的直径,把∠A为45°的直角三角尺ABC的一条直角边BC放在直线EF上,斜边AB所在直线与⊙O交于点P,点B,O重合,且AC大于OE.将三角尺ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是 13. 如图,在△ABC中,∠ACB= 130°,∠BAC=20°,BC=2.以C为圆心,CB为半径的圆交AB于点D,则BD的长为
13. 如图,在△ABC中,∠ACB= 130°,∠BAC=20°,BC=2.以C为圆心,CB为半径的圆交AB于点D,则BD的长为 14. 如图,AB是⊙O的直径,C是⊙O上的一点,OD⊥BC于点D.若BC=3,AB=5,则OD的长为
14. 如图,AB是⊙O的直径,C是⊙O上的一点,OD⊥BC于点D.若BC=3,AB=5,则OD的长为 15. 小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为cm.
15. 小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为cm.
三、解答题
-
16. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径.若∠ABC=50°,求∠CAD的度数.
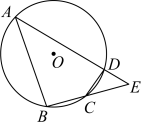
 17. 如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长.
17. 如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长. 18. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.
18. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.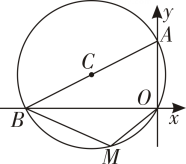 19. 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m.某天下雨后,排水管水面上升了0.2m,求此时排水管中水面宽CD的长.
19. 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m.某天下雨后,排水管水面上升了0.2m,求此时排水管中水面宽CD的长.
四、综合题
-
20. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
 (1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
(1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?