（人教版）2023-2024学年九年级数学上册 24.1 圆的有关性质 同步分层训练（基础卷）
试卷更新日期：2023-11-07 类型：同步测试
一、选择题
-
1. 如图，圆周角∠ACB =48°，则圆心角∠AOB的度数为（ ）．
A、48° B、24° C、96° D、90°2. 如图，AB是⊙O的直径，弦CD⊥AB于点E．若OC=5 cm，CD=6 cm，则AE=（ ）．
A、4cm B、3cm C、9cm D、8cm3. 如图，四边形ABCD内接于⊙O，四边形ABCO是平行四边形，则∠ADC的度数是（ ）．
A、45° B、50° C、60° D、75°4. 如图，延长圆内接四边形ABCD的边AB，DC，相交于点E，延长边AD，BC，相交于点F．若∠E=30°，∠F=50° ，则∠A的度数为（ ）．
A、20° B、30° C、50° D、60°5. 如图，BD是⊙O的直径，点A，C在⊙O上，= ， ∠AOB= 60°，则∠BDC的度数是（ ）
A、60° B、45° C、35° D、30°6. 如图，A，B，C，D是同一个圆上顺次任意四点，则图中相等的圆周角共有（ ）．
A、2对 B、4对 C、6对 D、8对7. 如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（ ）．
A、75° B、70° C、65° D、35°8. 如图，点A，B，C均在⊙O上．若∠A=66°，则∠OCB的度数是（ ）．
A、24° B、28° C、33° D、48°9. 下列说法正确的是（ ）．A、直径是圆的对称轴 B、与圆相交的直线是圆的对称轴 C、经过圆心的直线是圆的对称轴 D、与半径垂直的直线是圆的对称轴10. 如图所示为一名同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于A，B两点，他测得“图上”圆的半径为10厘米，厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟，则“图上”太阳升起的速度为（ ）.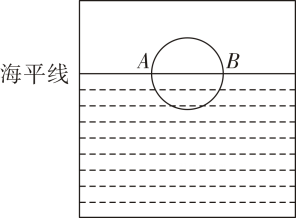
A、1.0厘米/分 B、0.8厘米/分 C、12厘米/分 D、1.4厘米/分二、填空题
-
11. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A，B的读数分别为86°，30°，则∠ACB的大小为
12. ⑴垂径定理由圆的轴对称性得到．⑵用垂径定理进行计算或证明时，常常通过作半径和构造直角三角形．
⑶“平分弦”“平分弧”“垂直弦”等条件常可联系到垂径定理的条件和结论的关系．
13. 如图所示，内接于.若的半径为2，则BC的长为.
14. 如图3-3所示为一条直径为2m的通水管道的轴截面，其水面宽1.6m，则这条管道中水最深为m.
15. ⊙O中，弦AB的长恰等于半径，则弧的度数是度．三、解答题
-
16. 如图所示，在⊙O的内接四边形ABCD中，AB=AD，∠C=100°.若点E在上，求∠E的度数.
17. 如图，A，C，B．D四点都在⊙O上，AB是⊙O的直径，且AB＝6，∠ACD＝45°，求弦AD的长．
18. 在直径是52cm的圆柱形油槽内装入一些油后，截面如图所示，如果油的最大深度CD为16cm，求油面宽度AB的长.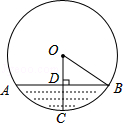
19. 已知：如图，在⊙O中， ， 与相交于点M，求证：.
20. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB＝20，CD＝16.求AE的长.
四、综合题
-
21. 如图，△ABC是⊙O的内接三角形，点C是优弧AB上一点（点C不与点A，B重合），设∠OAB=α，∠C=β．
(1)、当α=40º时，求β的度数；(2)、猜想α与β之间的关系，并给予证明
